Угол. Определение угла.

Два луча, исходящих из одной точки, ограничивают собой часть плоскости, которая расположена между лучам. Фигура, которая при этом образуется, называется углом. Лучи с общей вершиной в точке начала лучей, называются сторонами угла. Вершина угла расположена в точке начала лучей.

Угол – часть плоскости, ограниченная двумя лучами, исходящими из одной точки.

Угол – это геометрическая фигура, имеющая вершину, стороны и свою градусную меру.

Плоскость делится сторонами угла на две части. Меньший из углов называют внутренним, больший - внешним. Для того, чтобы не было разных толкований, о каком из углов идет речь, его стороны на чертеже соединяют дугой. (см. рисунок)

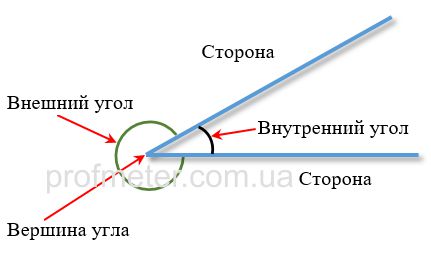
Угловая мера угла

• равным углам соответствует равная угловая мера;
• меньшему углу соответствует меньшая угловая мера;
• у угла, стороны которого совпадают (нулевого угла), угловая мера равна нулю (то же справедливо и для угла между параллельными прямыми);
• каждый ненулевой угол имеет определённую угловую меру, большую нуля;
• (аддитивность) угловая мера угла равна сумме угловых мер углов, на которые он разбивается любым лучом, проходящим между его сторонами (см. аксиома измерения углов).

Угол измеряют в градусах, радианах, градах и оборотах (подробнее см. статью "радианы и градусы").

1 оборот = 360 градусов = 2π радиан = 400 град

Рассмотрим угол, стороны которого совпадают (∠ВАВ₁). Его градусная мера равна 0° 

Если одну сторону угла (АВ) закрепить а вторую сторону (АВ₁) вращать против часовой стрелки до тех пор, пока она не совпадет с первой стороной (АВ), то плоскость такого угла составит полный угол (рис.5). Следовательно, угол А (обозначается ∠ А) – это полный угол.

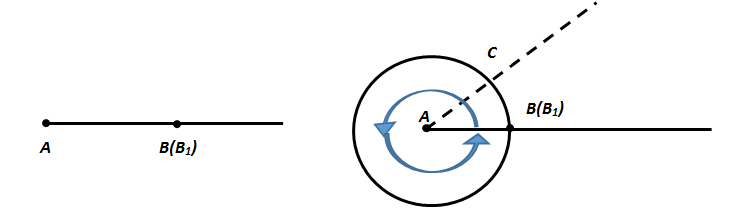
Обозначение углов

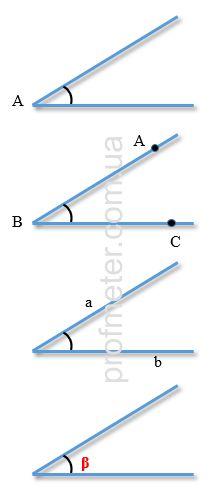
Угол может быть обозначен как комбинация знака угла и его вершины, например ∠А; (рис.1)

Также угол может обозначаться с помощью латинских заглавных букв. Например ∠ABC - это угол с вершиной B, стороны которого - это лучи BA и BC.(рис.2)

Может встречаться обозначение как значок угла с указанием сторон угла (например ∠ аb). (рис.3)

Угол может обозначаться греческими буквами α, β, γ и так далее. (рис.4) Исключение составляет только буква "π". Ее для обозначения углов не используют.

Градусная мера угла

Если взять полный угол и разделить его на 360 частей (углов), то каждая часть, составляющая 1/360  часть полного угла, называется угловым радиусом (обозначается 1°).

Следовательно, полный угол равен 1° *360=360°.

Половина полного угла составит развернутый угол, который равен 360°:2=180°.

Для того, чтобы подробнее узнать про радианы, градусы и перевод радиан в градусы см. статью "Радианы и градусы"

Центральный и вписанный в окружность угол

• Вписанные углы, опирающиеся на одну и ту же дугу окружности - равны.
• Величина вписанного угла, опирающегося на ту же самую дугу окружности, что и центральный угол, равна половине величины такого центрального угла.