|
|
Определение четырехугольника
Четырехугольник - это многоугольник с четырьмя вершинами, три из которых не лежат на одной прямой.
Четырехугольник - это геометрическая фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, последовательно соединенная отрезками.
Свойства четырехугольников
Четырехугольник может быть:
- Самопересекающимся
- Невыпуклым
- Выпуклым

Самопересекающийся четырехугольник - это четырехугольник, у которого любые из его сторон имеют точку пересечения (на рисунке синим цветом).
Невыпуклый четырехугольник - это четырехугольник, в котором один из внутренних углов более 180 градусов (на рисунке обозначен красным цветом)
Сумма углов любого четырехугольника, который не является самоперсекающимся всегда равна 360 градусов.
Особые виды четырехугольников
Четырехугольники могут обладать дополнительными свойствами, образуя особые виды геометрических фигур:
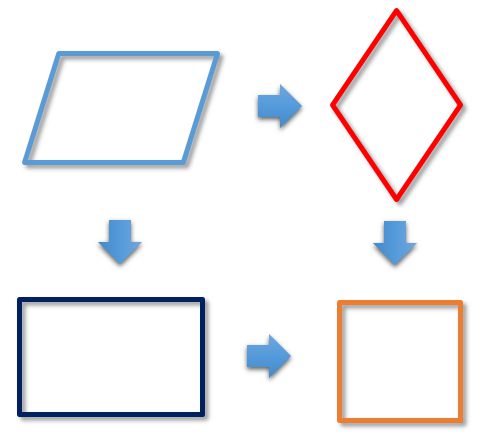
Подробнее о каждом из особых видов четырехугольника можно узнать, перейдя по ссылкам выше.
Как видно из рисунка, особые виды четырехугольников наследуют свойства своих "предков". Например, прямоугольник (на рисунке показан темно-синим цветом) является особым случаем параллелограмма (на рисунке показан голубым цветом). Таким образом, у него сохраняются все его свойства и добавляются свои, особенные. Поэтому при решении задач про прямоугольники можно применять все свойства и теоремы параллелограмма.
Квадрат (на рисунке показан оранжевым цветом) - частный случай прямоугольника. То есть квадрат имеет все свойства параллелограмма, прямоугольника, а также и свои, особенные. Но, самое интересное, квадрат также является частным случаем ромба (на рисунке показан красным цветом), то есть, кроме указанных (параллелограмм, прямоугольник), он обладает еще и всеми свойствами ромба.
Также, интересными особыми случаями четырехугольника являются трапеция и дельтоид.
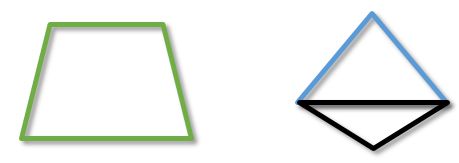
Четырехугольник и окружность
Четырехугольник, описанный вокруг окружности (окружность, вписанная в четырехугольник).
Главное свойство описанного четырехугольника:
Четырехугольник можно описать вокруг окружности тогда и только тогда, когда суммы длин противоположных сторон равны.
Четырехугольник, вписанный в окружность (окружность, описанная вокруг четырехугольника)
Главное свойство вписанного четырехугольника:
Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы противоположных углов равны 180 градусов.
Свойства длин сторон четырехугольника
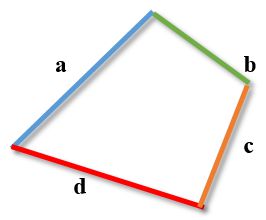
Модуль разности любых двух сторон четырёхугольника не превосходит суммы двух других его сторон.
|a -b| ≤ c + d
|a -c| ≤ b + d
|a -d| ≤ b + c
|b -c| ≤ a + d
|b -d| ≤ a + b
|c -d| ≤ a + b
Важно. Неравенство верно для любой комбинации сторон четырехугольника. Рисунок приведен исключительно для облегчения восприятия.
В любом четырёхугольнике сумма длин трёх его сторон не меньше длины четвёртой стороны.
a ≤ b + c + d
b ≤ a + c + d
c ≤ a + b + d
d ≤ a + b + c
Важно. При решении задач в пределах школьной программы можно использовать строгое неравенство (<). Равенство достигается только в случае, если четырехугольник является "вырожденным", то есть три его точки лежат на одной прямой. То есть эта ситуация не попадает под классическое определение четырехугольника.
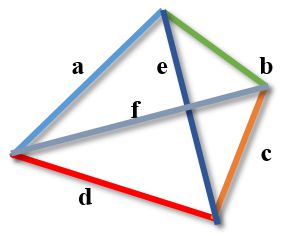
Соотношение сторон и диагоналей может быть выражено формулой
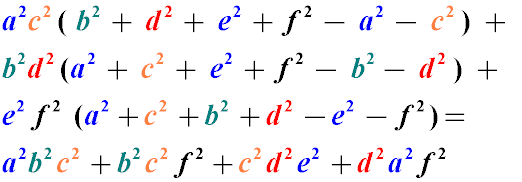
Неравенство Птолемея
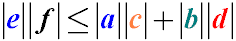
Произведение длин диагоналей четырехугольника меньше или равно сумме произведений противоположных сторон четырехугольника.
Теорема Гаусса
Если в четырёхугольнике две пары противоположных сторон не параллельны, то две середины его диагоналей лежат на прямой, которая проходит через середину отрезка, соединяющего две точки пересечения диагоналей и точку пересечения этих двух пар противоположных сторон.
Соотношение Бретшнайдера
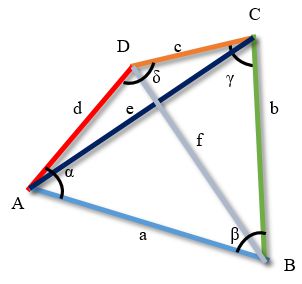
Произведение квадратов диагоналей произвольного несамопересекающегося четырехугольника равно сумме произведений квадратов его противоположных сторон минус удвоенное произведение всех его сторон, которое умножено на косинус суммы двух противоположных углов.
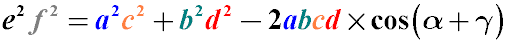
Формула Эйлера
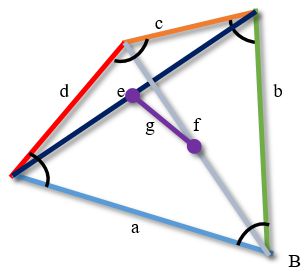
Квадрат двойного расстояния между серединами диагоналей произвольного несамопересекающегося четырехугольника равен сумме квадратов его сторон минус сумма квадратов его диагоналей
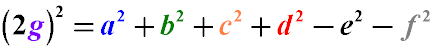
Средние линии четырехугольника
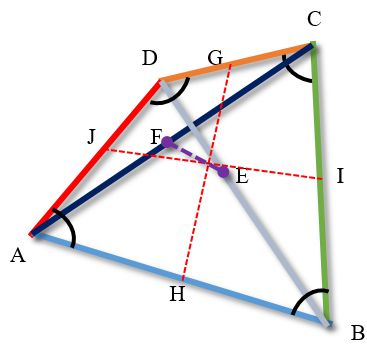
У каждого четырехугольника есть три средние линии.
Средними линиями несамопересекающегося четырехугольника называются отрезки, соединяющие середины его противолежащих сторон (первая и вторая) и отрезок, соединяющий середины его диагоналей.
На рисунке средние линии четырехугольника отмечены пунктирными линиями.
Центроид четырехугольника
Центроидом четырехугольника называется точка пересечения всех его средних линий.
Обобщенная теорема Ньютона
Средние линии несамопересекающегося четырехугольника, образуемые серединами противолежащих сторон (первая и вторая средняя линия) и отрезком, соединяющим середины диагоналей (третья средняя линия) пересекаются в одной точке и делятся ею пополам.
Прямая, проходящая через середины диагоналей четырехугольника и его центроид также называется прямой Ньютона.
(см. рисунок выше)
Теорема Вариньона
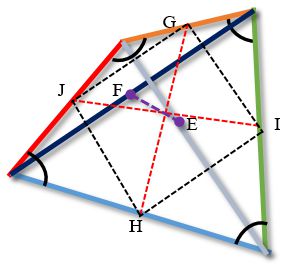
Четырёхугольники, которые образуются отрезками, соединяющими середины противолежащих сторон (GIHJ), а также середины диагоналей четырехугольника и середины противолежащих сторон (EHFG, JEIF) являются параллелограммами.
Эти параллелограммы называются параллелограммами Вариньона.
Четырехугольник, образованный серединами противолежащих сторон (на рисунке обозначен пунктирной линией GIHJ) называется большим параллелограммом Вариньона.
- Центры всех трёх параллелограммов Вариньона лежат на середине отрезка, соединяющего середины сторон исходного четырёхугольника (в этой же точке пересекаются отрезки, соединяющие середины противоположных сторон — диагонали вариньоновского параллелограмма).
-
Периметр большого параллелограмма Вариньона равен сумме диагоналей исходного четырёхугольника.
-
Площадь большого параллелограмма Вариньона равна половине площади исходного четырёхугольника
-
Площадь исходного четырёхугольника равна произведению первой и второй средних линий четырёхугольника на синус угла между ними
-
Сумма квадратов трёх средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей
Вписанная в треугольник окружность |
Описание курса
| Существование четырехугольника с заданными сторонами
|

