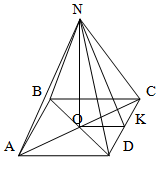
Решение.
Поскольку боковые ребра правильной четырехугольной пирамиды наклонены к основанию под углом 45 градусов, то в треугольнике ANC угол ANC равен 90 градусам. Таким образом, данный треугольник является прямоугольным.

Пусть длина ребра пирамиды равна а, тогда, исходя из того, что треугольник ANC - прямоугольный равнобедренный,
AC² = NC² + AN²
AC² = 2a²  
AC = a√2
откуда
OC = AC / 2  
OC =  a√2/2   

найдем высоту пирамиды NO: 
NO = √(NC² - OC² )
NO = √( a² - a²/2)
NO = a/√2

Рассмотрим прямоугольный треугольник COD и аналогичным способом найдем его высоту CK
CD² = OC² + OD² 
CD² = ( a√2/2 )²  +  ( a√2/2 )²
CD = a

Откуда
KC = CD / 2
KC = a / 2

OK² = OC² - KC ²
OK = a/2  

Теперь рассмотрим прямоугольный треугольник KON. Так как он прямоугольный, то
tg ∠NKO = NO / OK
tg ∠NKO = (  a/√2  ) / ( a / 2 )  
tg ∠NKO =   2/√2

откуда
∠NKO =  arctg( 2/√2 ) ≈ 54,7356°

Ответ:  arctg( 2/√2 ) ≈ 54,7356°