Призма

Данный раздел посвящен решению задач про призмы. Для успешного освоения данного раздела следует принять во внимание следующее.

Определение призмы

Призма - это объемный многогранник, две грани которого представляют собой равные (одинаковые) многоугольники, лежащие в параллельных плоскостях, а остальные грани представляют собой параллелограммы, противолежащие грани у которых являются общими с соответствующими сторонами параллельных многоугольников.

Ниже, на рисунке изображены треугольная, четырехугольная и наклонная четырехугольная призма. Обычно (но не обязательно) для упрощения понимания взаимного расположения оснований и их сторон, обозначения нижнего основания начинают латинскими буквами А, B, C и так далее, а соответствующие стороны верхнего основания обозначают теми же буквами с добавлением единицы - А1, B1, C1 и так далее.

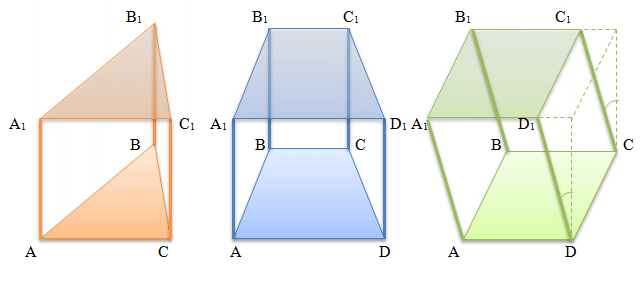
Другие определения призмы:

Призма - многогранник, основаниями которого являются равные многоугольники, соответствующие боковые грани которого представляют собой параллелограммы.

Другие определения:

Равные многоугольники, лежащие в параллельных плоскостях, называются основаниями призмы.

Грани призмы, соединяющие ее основания призмы (ABCD и A1B1C1D1), называются боковыми гранями. 

Площадь (объединение, совокупность) всех боковых граней призмы называется боковой поверхностью.

Общие грани параллелограммов, соединяющие основания призмы, называются боковыми ребрами. (AA1 BB1 CC1 и т.д.)

Длина отрезка, соединяющего основания призмы и перпендикулярного одновременно обоим основаниям, является (называется) высотой призмы.

Отрезок проведенный между двумя вершинами многогранника, представляющего собой призму, так, чтобы он не принадлежал ни одной плоскости призмы (основаниям или боковым граням) называется диагональю призмы. (АС1)

Плоскость, проходящая через боковое ребро призмы и диагональ основания (не путать с диагональю призмы!) называется диагональной плоскостью. (AA1C1C)

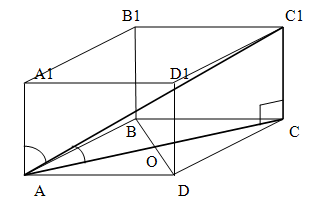
Свойства призмы

• Основания призмы равны
• Каждая из боковых граней обязательно является параллелограммом
• Боковые ребра призмы параллельны и равны между собой
• Боковые грани правильной призмы представляют собой равные прямоугольники
• При пересечении призмы и диагональной плоскости сечение представляет собой параллелограмм
• Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы
• Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах
• Перпендикулярное сечение перпендикулярно ко всем боковым граням

Специальные случаи призм

Параллелепипед - это призма, основанием которой является параллелограмм 

Прямоугольный параллелепипед - прямая призма, основанием которой является прямоугольник и все грани являются прямоугольниками

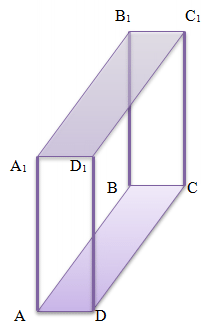
Прямая призма - призма, у которой боковые ребра перпендикулярны плоскости основания

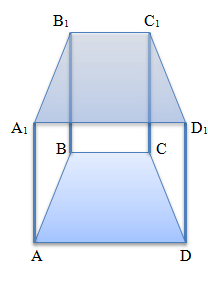
Правильная призма - это прямая призма, основаниями которой является правильный многоугольник. (см. также - правильная четырехугольная призма)

Куб - правильная призма, все стороны которой представляют собой правильный четырехугольник (квадрат)

Объем призмы

Формула нахождения объема призмы выглядит следующим образом:

V = Sh, где

V - объем призмы
S - площадь основания призмы
 h - высота призмы

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Площадь боковой поверхности произвольной призмы S=P х l, где P — периметр перпендикулярного сечения, l — длина бокового ребра.

Площадь боковой поверхности прямой призмы S=P х h, где P — периметр основания призмы, h — высота призмы.