|
|
Пояснение, как получаются тригонометрические тождества
Поясним, как выводятся тригонометрические тождества на примере очень простых формул:
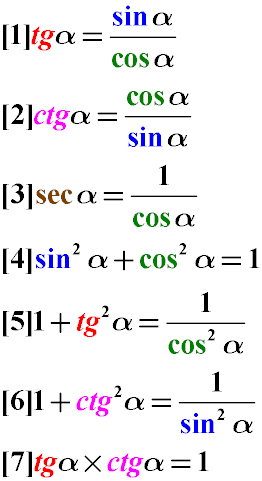
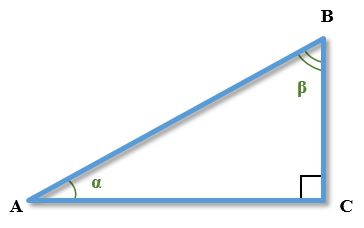
На примере прямоугольного треугольника ABC выведем простейшие тригонометрические тождества и докажем их правильность.
Доказательство тождества sin α / cos α = tg α
Поясним, как частное от деления синуса на косинус альфа дает тангенс этого же угла (Формула номер 1)
Из определения синуса следует, что
sin α = BC / AB
Из определения косинуса следует, что
cos α = AC / AB
Разделим одно выражение на второе
sin α / cos α
подставим вместо тригонометрических функций соотношение сторон, получим:
( BC / AB ) : (AC / AB)
При делении одной дроби на другую, подучим результат
sin α / cos α BC / AC
Из определения тангенса следует
tg α = BC / AC
Таким образом,
sin α / cos α = tg α
Тождество (1) доказано.
Краткое доказательство можно посмотреть на рисунке ниже:
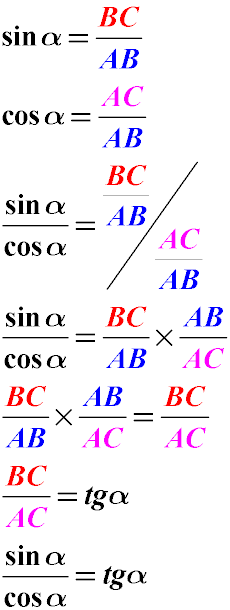
Тождества 2 и 3 доказываются абсолютно аналогичным способом.
Доказательство тождества sin2 α + cos2 α = 1
Теперь докажем тождество 4, что сумма квадрата синуса и косинуса одного и того же угла дает единицу.
Из определения синуса следует, что
sin α = BC / AB
Из определения косинуса следует, что
cos α = AC / AB
Возведем каждое выражение в квадрат и вычислим их сумму.
sin2 α + cos2 α = ( BC / AB )2 + ( AC / AB )2
поскольку обе дроби имеют один и тот же знаменатель, то
BC2 / AB2 + AC2 / AB2 = ( BC2 + AC2 ) / AB2
Снова посмотрим на рисунок выше.
BC2 + AC2 - это сумма квадратов катетов прямоугольного треугольника. Согласно, теореме Пифагора
BC2 + AC2 = AB2
Заменим числитель (BC2 + AC2) на тождественное выражение AB2 и получим:
AB2 / AB2 = 1
Таким образом,
sin2 α + cos2 α = 1
Тождество (4) доказано
Краткое доказательство можно посмотреть на рисунке ниже

Тригонометрические тождества и преобразования |
Описание курса
| Преобразования тригонометрических функций вида (α + a/bπ) и доказательство
|

