Цилиндр
ОПРЕДЕЛЕНИЕ ЦИЛИНДРА И ЕГО ЭЛЕМЕНТОВ
Цилиндр (круговой цилиндр) – тело, которое состоит их двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, - образующими цилиндра. Эти отрезки образуют цилиндрическую поверхность, являющуюся боковой поверхностью цилиндра.
Если основаниями цилиндра не являются круги, то цилиндр может быть эллиптическим. Обычно, такие виды цилиндра в элементарной геометрии не рассматриваются.
Альтернативное определение.
Цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя пересекающими ее параллельными плоскостями.
Полная поверхность цилиндра состоит из оснований и боковой поверхности.
Цилиндр называется прямым, если его образующие перпендикулярны к плоскости оснований.
Прямой цилиндр наглядно можно представить как тело, полученное в результате вращения прямоугольника вокруг стороны как оси.
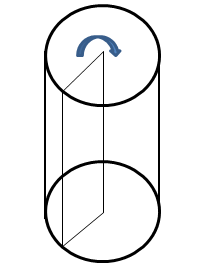
Радиусом цилиндра называется радиус его основания.
Высотой цилиндра называется расстояние между плоскостями его оснований.
Осью цилиндра называется прямая, проходящая через центры основания. Она параллельна образующим.
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник. Две стороны его – образующие цилиндра, а две другие – параллельные хорды оснований. Осевое сечение цилиндра – это сечение плоскостью, проходящей через его ось.
Касательной плоскостью к цилиндру называется плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
Объем цилиндра
Объем цилиндра равен произведению площади основания на высоту Н:
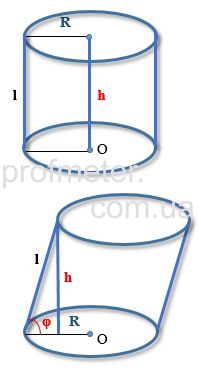
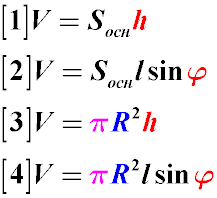
Если у цилиндра известны только площадь основания и образующая, то объем такого цилиндра будет равен произведению площади основания на образующую и синус угла между основанием и образующей [2].
Для цилиндра, в основании которого лежит круг, объем цилиндра будет равен площади круга на высоту [3][4].
Площадь боковой поверхности цилиндра
Площадь боковой поверхности прямого цилиндра с радиусом R основания и высотой Н
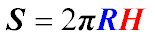
Соотношение объема шара и конуса |
Описание курса
| Задачи про цилиндр со вписанной призмой
|

