Геометрическое место точек. Метод геометрических мест
Определение: Геометрическим местом точек называется геометрическая фигура на плоскости, каждая точка которой обладает одним и тем же определенным свойством.
Метод геометрических мест применяется чаще всего при построениях. Например, серединный перпендикуляр к отрезку можно определить как геометрическое место точек, равноудаленных от точек концов отрезков; окружность можно определить как геометрическое место точек, равноудаленных от данной точки.
Теорема (о геометрическом месте точек). Геометрическое место точек, равноудаленных от двух данных точек, есть прямая, перпендикулярная отрезку, соединяющему эти точки, и проходящая через его середину.
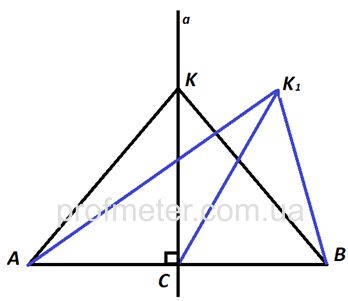
Доказательство. Пусть даны точки А и В, а точка С
– середина отрезка АВ. Нужно найти геометрическое место точек, равноудаленных от точек А и В.
Доказательство основано на свойстве серединного перпендикуляра к отрезку.
Серединный перпендикуляр СК, принадлежащий прямой а, как и любая точка этой прямой, - есть геометрическое место точек, равноудаленных от А и В, так как СКꓕАВ.
Допустим, что есть еще точка К1, расстояние до которой от А и В одинаково.
Рассмотрим ∆АК1В, он разбит отрезком К1С
на два треугольника: ∆АК1С и ∆К1СВ. Если эти треугольники равны, то точка К1
тоже удалена на одинаковое расстояние от А и В.
Через точку С проходят две прямые СК
и СК1. На основании теоремы 16 (о единственности перпендикуляра из точки к прямой), если СКꓕАВ
по построению, то СК1 не может быть перпендикулярна АВ.
Так как из двух смежных углов (∟К1СА и ∟К1СВ) один должен быть острый, а второй – тупой, то ∆К1СА≠∆К1СВ, следовательно, К1А≠К1В (есть две равные стороны, АС=ВС
и К1С
– общая, но нет равных углов между ними), значит, К1С – наклонная к АВ и АК1≠ВК1.
Метод геометрических мест
Определение: Сущность метода геометрических мест в том, что при наличии не одного, а нескольких условий для построения геометрической фигуры, нужно построить несколько геометрических фигур, которые по очереди будут удовлетворять каждому из условий, а потом найти такое геометрическое место точек, которое при пересечении или совмещении этих фигур будет удовлетворять всем условиям построения.
Например: Даны три точки: А, В, С.
Построить точку Х, равноудаленную от А и В и находящуюся на расстоянии h от точки С.
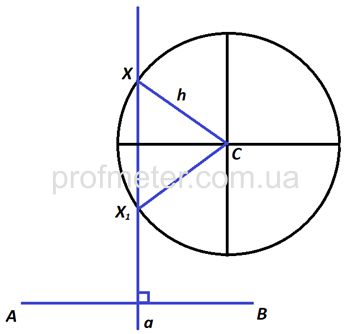
Порядок построения:
1.Построим геометрическое место точек, удовлетворяющее первому условию: это будет серединный перпендикуляр к отрезку АВ. Прямая а, которая содержит серединный перпендикуляр к отрезку АВ, удовлетворяет полностью первому условию.
2.На перпендикуляре (прямая а) должна находится точка Х, которая удовлетворяла бы второму условию (расстояние от нее до С должно составлять h).
Если из точки С
радиусом h провести окружность, то все точки окружности будут расположены от С на одинаковом расстоянии h (построили второе геометрическое место точек, равноудаленных от С).
3.Пересечение первого геометрического места точек (прямая а) и второго (окружности с центром в точке С) будет удовлетворять обоим условиям задачи. Точки пересечения окружности и прямой (Х1
и Х) и будут теми искомыми точками, которые равноудалены от точек А
и В
и находятся от С на расстоянии h.
Точки, отрезки и прямые |
Описание курса
| Отрезки в координатной плоскости
|

