|
|
Тригонометрический круг
Тригонометрический круг - это окружность с единичным радиусом и центром в начале осей координат, каждая точка которой образует треугольник с точками:
- точка в начале осей координат (точка 0;0)
- точка на окружности (выбрана нами)
- точка на оси X, которая является проекцией выбранной нами точки на эту ось (перпендикуляр к оси X)
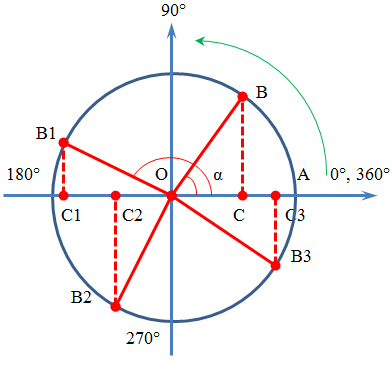
Как видно, такой треугольник является прямоугольным, так как из выбранной нами точки на ось абсцисс всегда опускается перпендикуляр. То есть сторона, соединяющая начало координат и выбранную нами точку на тригонометрическом круге ( на приведенном рисунке обозначенную как B, B1. B2, B3) всегда является гипотенузой прямоугольного треугольника, проекция выбранной точки - это катет, а сторона от точки пересечения с осью X образует второй катет.
Угол, который образуется между осью абсцисс (осью X) и гипотенузой треугольника - является углом, для которого и вычисляются значения тригонометрических функций. Этот угол отсчитывается от положительного направления оси абсцисс (оси X) как ноль, далее против часовой стрелки. Таким образом, полный круг составляет 360 градусов или 2π радиан.
Чтобы вычислить значение тригонометрической функции для выбранного угла тригонометрического круга достаточно воспользоваться координатами точки, принадлежащей окружности тригонометрического круга. На приведенном выше рисунке, показано вычисление значения синуса для всех углов.
Например, sin α для треугольника OBC (где координаты точки B равны (x,y) ) ,будет равен: y / √ ( x2 + y2)
Свойства тригонометрического круга
Если последовательно вычислять значения тригонометрических функций для тригонометрического круга, то становится видно, что результат таких вычислений меняет свой знак в зависимости от того, в какой четверти тригонометрического круга выбрана точка. При этом знак тригонометрической функции в пределах одной и той же четверти сохраняется.
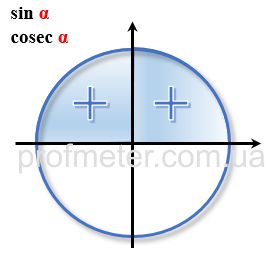
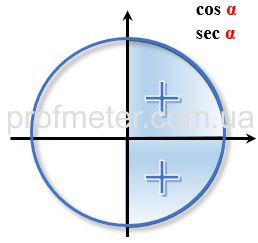
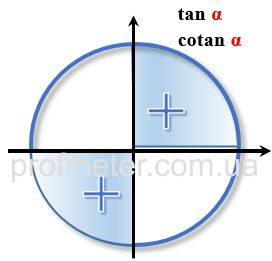
Знаки тригонометрических функций в координатных четвертях в тригонометрическом круге
Преобразование углов больше 360 градусов или 2π радиан
Как видно из картинок, после того, как значение угла превысит 360 градусов (или 2π радиан), то результат вычисления значения будет тем же самым. То есть, для того, чтобы привести значение к "нормальному" - нужно вычесть из имеющегося значения 360 градусов или 2π радиан и повторять операцию столько раз, пока результат не станет меньше 360 или 2π.
Тригонометрические соотношения в прямоугольном треугольнике |
Описание курса
| Радианы и градусы. Радiани i градуси
|

