Основанием прямой призмы ABCD A₁B₁C₁D₁ является параллелограмм ABCD со сторонами 4 см и 4√3 см и углом, равным 30 градусов. Диагональ AC₁ призмы образует с плоскостью основания угол в 60 градусов. Найдите площадь боковой поверхности призмы.

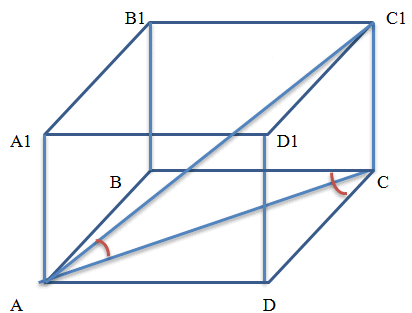
Решение.
Поскольку сумма соседних углов параллелограмма равна 180 градусам, то углы B и D. будут равны 180 - 30 = 150 градусов.
(свойства параллелограмма можно посмотреть в уроке "параллелограмм")
Диагональ параллелограмма AC, таким образом, образует треугольник ACD с углом C равным 150 градусов.
Применим теорему косинусов, при этом обозначив диагональ параллелограмма как d, а  стороны параллелограмма как a и b. Учтем, что косинус 150 градусов равен cos( 150° ) = -√3 / 2. Получим:
d² = a² + b² - 2abcos( 150° )
d² = 16 + 48 - 2 * 4 * 4√3 * ( -√3 / 2 ) = 112  
d = 4√7
AC =  4√7  

Зная величину диагонали параллелограмма, найдем высоту параллелограмма. Треугольник, который образует диагональ AC₁ ( AC₁С ) с основанием призмы, согласно условию задачи (призма - прямая) является прямоугольным. Угол ∠C₁AC по условию равен 60 градусов. Для прямоугольного треугольника тангенс угла ∠C₁AC равен отношению противолежащего катета к прилежащему, то есть tg ( ∠C₁AC ) = C₁С / AC . Учтем, что тангенс 60 градусов равен tg 60° = √3.
Соответственно, C₁С =  AC tg ( ∠C₁AC )
C₁С = 4√7 * tg 60°
C₁С = 4√21

Зная высоту призмы, определим площадь ее боковой поверхности:
S = 2ha + 2hb
S = 2 * 4 √21 * 4 √3 + 2 * 4 √21 * 4 = 96√7 + 16√21 ≈ 327,31  

Ответ: 96√7 + 16√21 ≈ 327,31