Шестиугольник - это многоугольник, общее количество углов (вершин) которого равно шести.

Выпуклый шестиугольник - это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.

При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.

Правильный шестиугольник

Правильный шестиугольник - это шестиугольник, все стороны которого равны между собой.

Свойства правильного шестиугольника

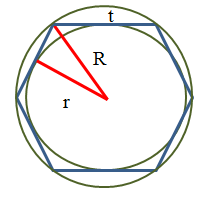
все внутренние углы равны между собой  каждый внутренний угол правильного шестиугольника равен 120 градусам  все стороны равны между собой  сторона правильного шестиугольника равна радиусу описанной окружности  правильный шестиугольник заполняет плоскость без пробелов и наложений

всі внутрішні кути рівні між собою  кожен внутрішній кут правильного шестикутника дорівнює 120 градусам  всі сторони рівні між собою сторона правильного шестикутника дорівнює радіусу описаного кола  правильний шестикутник заповнює плоскість без пропусків і накладень

Формулы для правильного шестиугольника

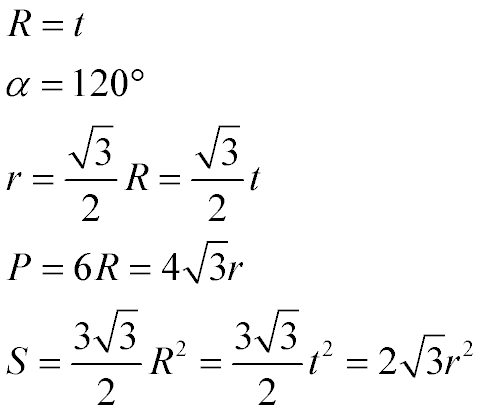
(по порядку следования формул)

• Радиус описанной окружности (R) правильного шестиугольника равен его стороне (t)
• Все внутренние углы равны 120 градусам
• Радиус вписанной окружности (r) равен корню из трех, деленному на два и умноженному на длину стороны t (радиус описанной окружности R)
• Периметр правильного шестиугольника (P) равен шести радиусам описанной окружности (R) или четыре корня из трех, умноженным на радиус вписанной окружности (r)
• Площадь правильного шестиугольника равна трем корням из трех пополам, умноженным на квадрат радиуса описанной окружности (R) или квадрат стороны (t); либо площадь правильного шестиугольника равна двум корням из трех, умноженным на квадрат радиуса вписанной окружности (t)

Задача