Примечание. Текст задачи взят с форума.

Задача.
Катет прямоугольного треугольника равен 8 см,а прилежащий к нему угол 60 градусов. Расстояние от точки пространства до всех вершин треугольника равно по 10 см.Найти расстояние от этой точки до плоскости треугольника.

Решение.

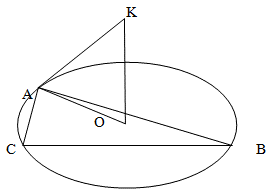
Пусть AC = 8, ∠CAB = 60°

Исходя из того, что, что расстояние от точки пространства К до вершин треугольника одинаковое, то вершина К будет проецироваться в центр описанной вокруг прямоугольного треугольника окружности. Таким образом, решение задачи сводится к тому, чтобы найти высоту перпендикуляра, проведенного из центра описанной окружности.

Формула радиуса описанной окружности R = a / 2sinα

откуда
R = AC / ( 2 sin ∠ABC )

Поскольку треугольник прямоугольный, а один из углов (прилежащий) известен, то противолежащий угол будет равен:
∠ABC = 180° - 90° - 60°  = 30° 

R = 8 / ( 2 sin 30 ° ) = 8 см

Теперь найдем высоту получившегося прямоугольного треугольника AOK

OK = √ (10² - 8² ) = √36 = 6

Ответ: 6 см