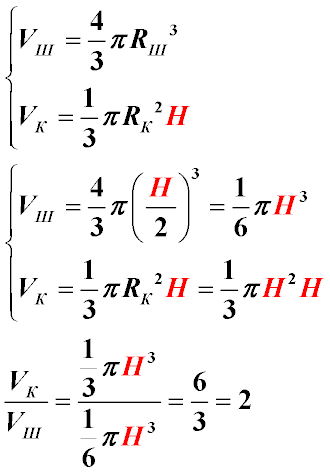 | Итерация 1. Запишем стандартные формулы нахождения объема. Формулу объема шара и формулу нахождения объема конуса.
Итерация 2. Основными параметрами для обеих формул являются радиус окружности, а для конуса также и его высота. Поскольку, по условию задачи, диаметр шара равен высоте конуса, то радиус шара будет равен половине его высоты. Поэтому заменим в первоначальной формуле радиус (Rш) шара на половину высоты конуса и получим формулу, указанную во второй итерации (см. на рисунке с решением). Упростив выражение, получим, что объем шара по условию задачи будет равен одной шестой пи, умноженной на высоту конуса в кубе.
Теперь рассмотрим конус. По условию задачи образующая с плоскостью основания составляет угол в 45 градусов. Исходя из этого, Высота, радиус основания конуса и его образующая составляют прямоугольный треугольник с углами 45, 45 и 90 градусов (сумма углов треугольника 180 градусов, высота с основанием образуют прямой угол, второй угол дан по условию). Таким образом, отношение высоты к радиусу основания конуса (H/R) является тангенсом угла, который составляет образующая и основание, то есть tg 45 градусов. Из таблицы значений тригонометрических функций выясняем, что тангенс 45 градусов равен единице. Если H / R = 1, то H = R. Заменим R на H в исходной формуле и получим, что для нашего случая, описанного в задаче, объем конуса будет равен одной трети пи, умноженной на высоту в кубе.
Итерация 3. Теперь разделим объем конуса на объем шара, подставив формулы, полученные из итерации 2. После сокращения дроби получаем ответ - 2.
Ответ: Соотношение объемов конуса и шара равно 2:1 | Ітерація 1. Запишемо стандартні формули знаходження об'єму. Формулу об'єму кулі і формулу знаходження об'єму конуса.
Ітерація 2. Основними параметрами для обох формул є радіус кола, а для конуса також і його висота. Оскільки, по умові завдання, діаметр кулі дорівнює висоті конуса, то радіус кулі дорівнюватиме половині його висоти. Тому замінимо в первинній формулі радіус (Rш) кулі на половину висоти конуса і отримаємо формулу, вказану в другій ітерації (див. на малюнку з рішенням). Спростивши вираження, отримаємо, що об'єм кулі по умовам завдання буде рівний одной шостой пі, помноженой на висоту в кубi.
Тепер розглянемо конус. По умові завдання твірна з плоскістю основи складає кут в 45 градусів. Виходячи з цього, Висота, радіус основи конуса і його твірна складають прямокутний трикутник з кутами 45, 45 і 90 градусів (сума кутів трикутника 180 градусів, висота з основою утворюють прямий кут, другий кут дан по умові). Таким чином, відношення висоти до радіусу основи конуса (H/R) є тангенсом кута, який складає твірна і підстава, тобто tg 45 градусів. З таблиці значень тригонометричних функцій з'ясовуємо, що тангенс 45 градусів дорівнює одиниці. Якщо H / R = 1, то H = R. Замінимо R на H у вихідній формулі і отримаємо, що для нашого випадку, описаного в завданні, об'єм конуса дорівнюватиме одній третині пі, помноженій на висоту в кубі.
Ітерація 3. Тепер розділимо об'єм конуса на об'єм кулі, підставивши формули, отримані з ітерації 2. Після скорочення дробу отримуємо відповідь - 2.
Відповідь: Співвідношення об'ємів конуса і кулі дорівнює 2:1 |

