|
|
Примечание. Это урок с задачами по геометрии о подобии треугольников. Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.
Задача
В треугольнике ABC угол A вдвое больше угла B, а длины противолежащих этим углам сторон соответственно равны 12 и 8. Найти третью сторону.
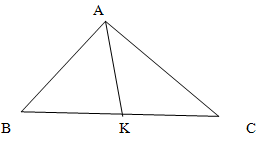
Решение.
Для угла А построим биссектрису на противоположную сторону BC. Пусть она пересечет противоположную сторону в точке К.
Исходя из того, что AK - биссектриса, углы ABC и KAC - равны. Поскольку угол С у них общий, то и третий угол этих треугольников является одинаковым. Таким образом, треугольники являются подобными по трем углам.
Исходя из того, что треугольники ABC и AKC подобны:
AC : BC = KC : AC = AK : AB
AC : BC = KC : AC
8 / 12 = KC / 8
KC = 64 / 12 = 16 / 3
Поскольку угол AKB = ABK (BK - биссектрисса, следовательно - треугольник AKB равнобедренный)
Откуда AK = BK
Учтем, что BK = AC - KC, тогда
AK = BK = 12 - 16 / 3
Теперь вернемся к свойствам подобных треугольников
KC : AC = AK : AB
и подставим известные значения
(16 / 3 ) / 8 = ( 12 - 16 / 3 ) / AB
AB = (AK * AC) / KC = 10
Ответ: 10 см
Простейшие задачи на подобие треугольников |
Описание курса
| Подобие треугольников. Третий признак подобия
|

