АКСИОМА 1. СВОЙСТВА ПРИНАДЛЕЖНОСТИ ТОЧЕК И ПРЯМЫХ НА ПЛОСКОСТИ

Какова бы ни была прямая, существуют точки принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.

Данное утверждение является аксиомой, то есть оно изначально принимается как верное и доказательству не подлежит.

Комментарии

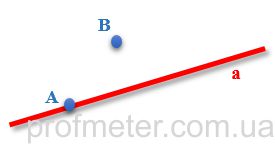
На рисунке ниже, обозначены точки A и B. При этом точка A принадлежит прямой a, а точка B - не принадлежит. Точки обозначены синим цветом, прямая - красным.

Примечание. Точки на рисунках обычно обозначаются заглавными буквами, а прямые - строчными.

Если точка принадлежит прямой (Рис.1), то краткая запись такая: А  ∈ а (читается как: «точка А принадлежит прямой «а»). Если точка не принадлежит прямой, то краткая запись такая: В ∉ а (читается как: «точка В не принадлежит прямой а»).

Если взять две несовпадающие точки (А и С), то через них можно провести только одну прямую (а), хотя через каждую из этих точек можно провести бесчисленное множество прямых (Рис.2)

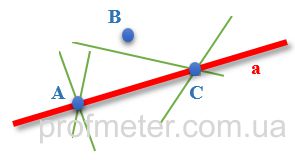
Примечание. Когда прямой принадлежат две точки (в данном случае A и C ), то она может быть также описана как прямая AC, при этом нужно понимать, что обозначение a (строчная буква a) и AC относится к одной и той же прямой.
Пояснение. Поскольку через две точки (см. аксиому) можно провести только одну прямую, то обозначений этой прямой может быть несколько, а смысл остается тем же самым.

Если точки А и С совпадают (на чертеже в этом случае одна точка будет обозначена двумя буквами), то через них можно провести бесчисленное множество прямых.

Описанная выше аксиома является базовой для Евклидовой геометрии. На основании данной аксиомы строятся доказательства многих теорем.