АКСИОМА 3. СВОЙСТВА ИЗМЕРЕНИЯ ОТРЕЗКОВ

Каждый отрезок имеет определенную длину, бóльшую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Данное утверждение является аксиомой, то есть оно изначально принимается как верное и доказательству не подлежит.

Комментарий

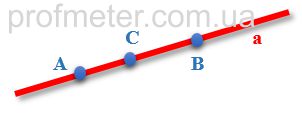
Возьмем прямую a и обозначим на ней точки A и B, которые образуют отрезок AB, принадлежащий этой прямой. Поскольку точки A и B не совпадают, то длина отрезка AB больше нуля.

Если на отрезке взять любую точку, кроме точек начала и конца отрезка, то отрезок разбивается этой точкой на два отрезка и его длина равна сумме длин этих отрезков. 

Между точками A и B обозначим точку C, которая разобьет отрезок AB на две части - AC и CB. 

Длина отрезка АВ равна сумме длин отрезков АС и СВ:

АВ=АС+СВ

В этом и состоит утверждение аксиомы.

Длина каждого из полученных отрезков равна разности длин целого отрезка (АВ) и его второй части (СВ или АС).

АС=АВ-СВ и СВ=АВ-АС

На основании утверждения этой аксиомы построено доказательство большинства теорем планиметрии и стереометрии.

Измерение отрезков

Измерить отрезок — это значит установить его длину в определенных единицах.
Например, это могут быть миллиметр (мм), сантиметр (см), дециметр (дм), метр (м), километр (км). Между единицами длины принято такое соотношение:

• 1 см = 10 мм;
• 1 дм = 10 см = 100 мм;
• 1 м = 10 дм = 100 см = 1 000 мм;
• 1 км =1 000 м.