|
Примечание. Для получения справочной информации см. также формулы преобразования тригонометрических функций.
Общий принцип преобразования функций вида α + a/bπ к более простому виду
Чтобы осуществить приведение угла тригонометрической функции, необходимо представить аргумент функции в виде:
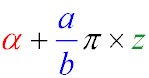
После этого можно будет воспользоваться правилами и формулами, которые указаны ниже.
Правило 1. Если a=2, а z - натуральное число, то название функции не меняется
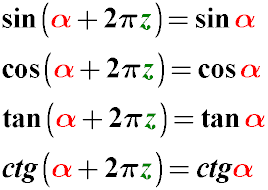
Синус альфа плюс два пи будет равен синус альфа.
Косинус альфа плюс два пи будет равен косинус альфа.
Тангенс альфа плюс два пи будет равен тангенс альфа.
Котангенс альфа плюс два пи будет равен котангенс альфа.
Данные равенства следуют из свойств тригонометрического круга.
Пример. Приведем к более простому виду выражение cos 390.
Примем во внимание, что π = 180 градусов, тогда
cos 390 = cos ( 30 + 2π )
Теперь воспользуемся формулой (2) приведения на рисунке выше
cos ( 30 + 2π) = cos 30
Правило 2. Вычитание из 2π угла α
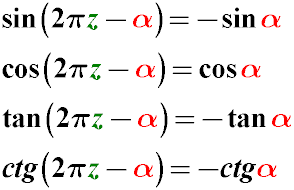
Синус два пи минус альфа будет равен минус синус альфа.
Косинус два пи минус альфа равен косинус альфа.
Тангенс два пи минус альфа равен минус тангенс альфа.
Котангенс два пи минус альфа равен минус котангенс альфа.
Данные свойства вытекают из свойств тригонометрического круга с учетом четности функций.
Пример. Приведем к более простому виду выражение sin 345.
Примем во внимание, что π = 180 градусов, тогда
sin 345 = sin ( 2π - 15 )
Теперь воспользуемся формулой (1) приведения на рисунке выше, тогда
sin ( 2π - 15 ) = - sin 15
Правило 3. Сложение угла с π/2
Если аргумент тригонометрической функции содержит выражение π/2 или n*π/2, где n - натуральное нечетное число, то функция
меняется по следующим правилам:
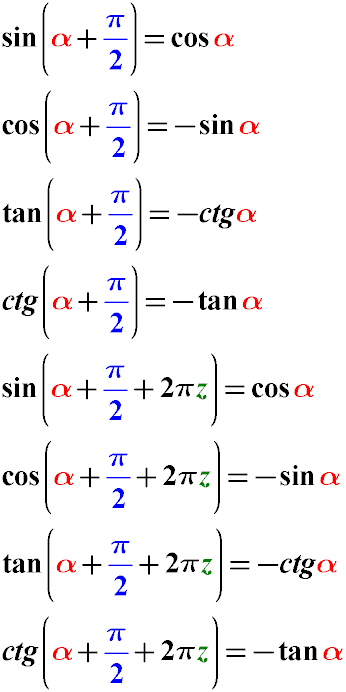
Синус угла альфа плюс пи на два равен косинусу того же угла.
Косинус альфа плюс пи на два равен минус косинус альфа.
Тангенс альфа плюс пи на два равен минус котангенс альфа.
Котангенс альфа плюс пи на два равен минус тангенс альфа.
Из свойств тригонометрического круга следует, что:
Синус угла альфа плюс пи на два плюс два пи равен косинусу того же угла.
Косинус альфа плюс пи на два плюс два пи равен минус косинус альфа.
Тангенс альфа плюс пи на два плюс два пи равен минус котангенс альфа.
Котангенс альфа плюс пи на два плюс два пи равен минус тангенс альфа.
Пример. Приведем к более простому виду выражение sin ( α + 5π/2 ).
sin ( α + 5π/2 ) = sin (α + π/2 + 2π*1)
sin (α + π/2 + 2π*1) = cos α
Правило 4. Формулы вычитания угла из π/2 (π/2 - α)
Если в аргументе тригонометрической функции есть вычитание угла из значения π/2, например cos( π/2 - α ),
тогда можно воспользоваться следующими формулами преобразования аргумента:
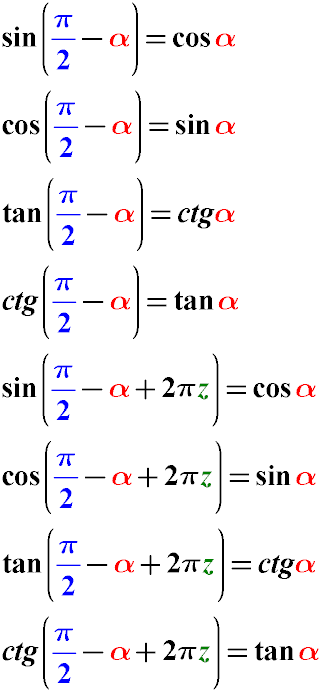
Из свойств прямоугольного треугольника следует, что:
Синус угла пи на два минус альфа равен косинусу альфа.
Синус угла пи на два минус альфа равен синусу альфа.
Тангенс пи на два минус альфа равен конангенсу альфа.
Котангенс угла пи на два минус альфа равен тангенсу альфа.
Из свойств тригонометрического круга следует, что:
Синус угла пи на два минус альфа плюс два пи равен косинусу альфа.
Синус угла пи на два минус альфа плюс два пи равен синусу альфа.
Тангенс пи на два минус альфа плюс два пи равен конангенсу альфа.
Котангенс угла пи на два минус альфа плюс два пи равен тангенсу альфа.
Пример. Приведем к более простому виду выражение cos ( 5π/2 - α ).
cos ( 5π/2 - α ) = cos( π/2 - α + 2π * 1)
cos( π/2 - α + 2π * 1) = sin α
Правило 5. Тригонометрические формулы приведения угла α + π
Если аргумент тригонометрической функции можно представить как сумму углов вида α + π + 2πz, то такая функция может быть
приведена к более простому виду с помощью следующих формул:
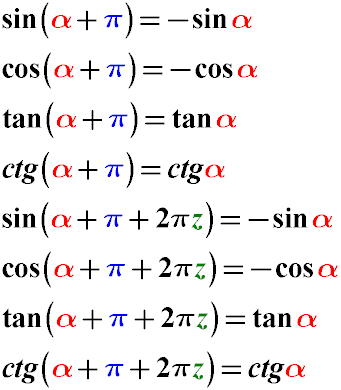
Синус альфа плюс пи равен минус синус альфа.
Косинус альфа плюс пи равен минус косинус альфа.
Тангенс альфа плюс пи равен тангенс альфа.
Контангенс альфа плюс пи равен котангенс альфа.
также
Синус альфа плюс пи плюс два пи равен минус синус альфа.
Косинус альфа плюс пи плюс два пи равен минус косинус альфа.
Пример. Приведем к более простому виду выражение sin (7π + α)
sin (7π + α) = sin ( π + α + 2π * 3)
sin ( π + α + 2π * 3) = - sin α
Правило 6. Тригонометрические формулы приведения для угла ( π - α )
Если в аргументе тригонометрической функции нужно вычесть угол из π, то есть упростить аргумент функции вида ( π - α ),
можно воспользоваться следующими формулами:
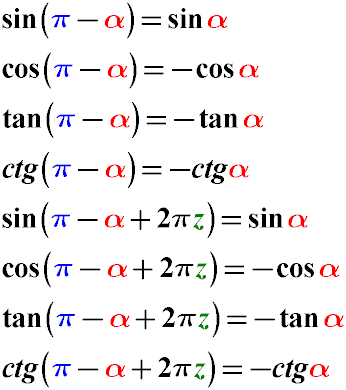
Пример. Приведем к более простому виду выражение sin ( 5π - α ).
sin ( 5π - α ) = sin ( π - α + 2π * 2 )
sin ( π - α + 2π * 2 ) = sin α
Правило 7. Тригонометрические формулы приведения функций для углов ( 3π / 2 + α )
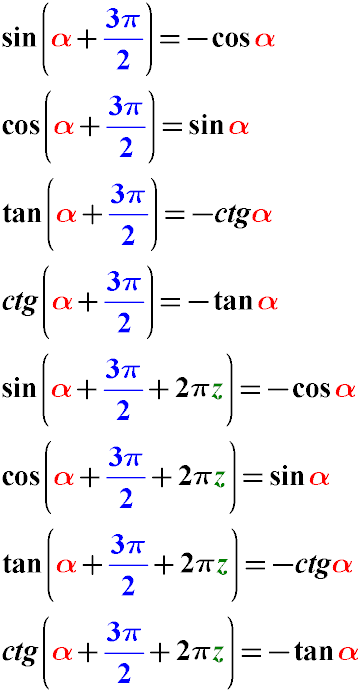
Пример. Приведем выражение cos (α + 7π/2) к более простому виду.
cos (α + 7π/2) = cos (α + 3π/2 + 2π * 1)
cos (α + 3π/2 + 2π * 1) = sin α
Правило 8. Тригонометрические формулы приведения аргумента для случаев вычитания угла α из 3 π / 2
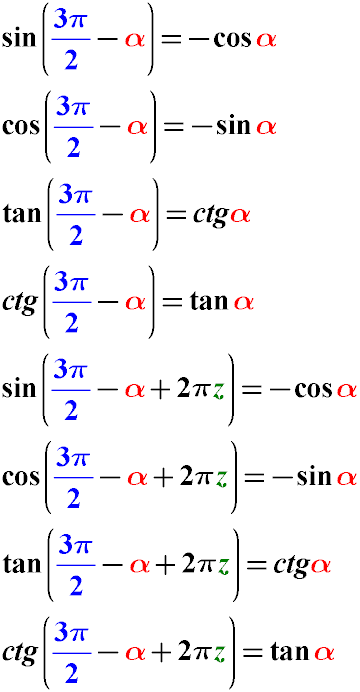
Пример. Приведем выражение sin ( 7π/2 - α ) к более простому виду.
sin ( 7π/2 - α ) = sin( 3π/2 - α + 2π * 1)
sin( 3π/2 - α + 2π * 1) = - cos α
Доказательство правильности формул преобразования тригонометрических функций вида (α + a/bπ)
ЗНАЧЕНИЯ СИНУСА, КОСИНУСА И ТАНГЕНСА ОСТРЫХ УГЛОВ
Значения тригонометрических функций острых углов выводятся из соотношения сторон прямоугольного треугольника.
ТЕОРЕМА: Для любого острого угла α:
sin (90°- α)=cos α;
cos (90°- α)=sin α;
tg (90°- α)=ctg α.
Рассмотрим прямоугольный треугольник с острым углом α. По теореме Пифагора:
АС2=АВ2+ВС2.
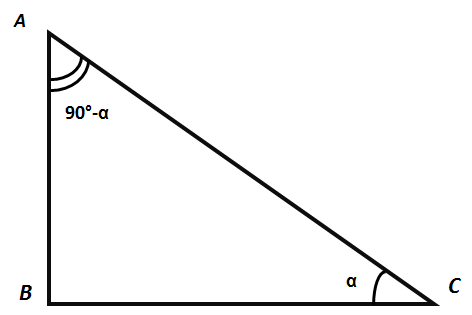
По определению тригонометрических функций:
sin α= АВ/АС и cos α= ВС/АС (1)
Так как ∠А + ∠С = 90°, то
∠А = 90°- ∠С
∠ А=90°-α,
sin (90°-α)=ВС/АС и cos (90°-α)=АВ/АС (2)
Сравним равенства (1) и (2) и запишем тождественные равенства:
sin (90°-α) = cos α; cos (90°-α) = sin α. (3)
Вычислим tg (90°- α), зная, что тангенс угла равен отношению синуса и косинуса того же угла и используя равенства (3):
tg (90°-α) = sin(90°-α) / cos(90°-α) =cos α / sin α = ctg α.
Пояснение (доказательство) простейших тригонометрических тождеств |
Описание курса
| Тригонометрические формулы понижения степени sin cos tg
|

