|
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение.
См. также - цилиндр и формулы объема цилиндра и площади боковой поверхности.
Задача. Призма, вписанная в цилиндр
В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 60 градусам. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45 градусов. Найдите объем цилиндра.

Решение.
Объем цилиндра найдем по формуле:
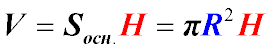
где:
R - радиус основания прямого цилиндра,
h - высота.
Найдем основание цилиндра. 1-й способ.
Основание цилиндра одновременно является окружностью, описанной вокруг прямоугольного треугольника, являющегося основанием призмы. Диаметр окружности, описанной вокруг прямоугольного треугольника, лежит на его гипотенузе. То есть длина гипотенузы равна 2R.
Радиус окружности, описанной вокруг треугольника найдем по формуле:
R = x / 2 sin α
где:
x - сторона треугольника
α - угол, противолежащий стороне а.
Противолежащий угол найдем следующим образом. Поскольку треугольник прямоугольный, то противолежащий катету угол будет равен 180-90-60 = 30 градусов. Таким образом, радиус описанной окружности (он же радиус цилиндра) равен:
R = 2a / 2 sin 30 = 2a
Найдем основание цилиндра. 2-й способ
У прямоугольного треугольника гипотенуза одновременно является диаметром описанной окружности. Половина гипотенузы будет равна ее радиусу.
Таким образом найдем гипотенузу для прямоугольного треугольника, зная угол и его катет через тригонометрическую функцию:
2R = 2a / cos 60 = 2a / 0.5 = 4a
R = 2a
Найдем высоту цилиндра.
Диаметр описанной окружности образует с диагональю призмы прямоугольный треугольник, один катет которого является диаметром описанной окружности, второй - высотой цилиндра и призмы, а гипотенуза является диагональю большей стороны призмы и одновременно цилиндра.
Поскольку угол диагонали с основанием составляет 45 градусов, то второй угол равен 180 - 45 - 90 = 45 градусов.
Исходя из того, что прямоугольный треугольник равнобедренный, то высота цилиндра и призмы равна диаметру окружности. Таким образом:
V = пR2h
V = п*4a2*4a
V = п16a3.
Ответ: п16a3.
Задача. В цилиндр вписана правильная шестиугольная призма
В цилиндр вписана правильная шестиугольная призма. Найти угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.
Решение.
Если радиус основания равен высоте цилиндра, диагональ боковой грани правильной шестиугольной призмы представляет собой прямоугольный треугольник, у которого один из катетов равен высоте цилиндра (r), а второй катет равен стороне шестиугольника, вписанного в окружность.Согласно свойствам шестиугольника, вписанного в окружность, его сторона равна радиусу такой окружности.
То есть, каждая боковая грань данной вписанной призмы – квадрат. Диагональ грани образует с осью цилиндра, как и с боковым ребром, одинаковый угол 45°, так как ось цилиндра и боковые ребра вписанной призмы параллельны.
Цилиндр |
Описание курса
| Цилиндр и его сечения
|

