Синус, косинус и тангенс угла 105 градусов

Синус 105 градусов, косинус 105 градусов, тангенс 105 градусов

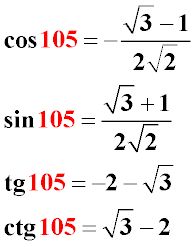
Как найти значения тригонометрических функций для угла 105 градусов

Найдем значения синуса, косинуса и тангенса для угла 105 градусов аналитическим способом.
На первый взгляд, нахождение значений синуса, косинуса и тангенса для угла 105 градусов - задача сложная. Однако, это не совсем так.
Прежде всего, мы должны обратить внимание, что для углов, значения которых превышают 90 градусов, у нас есть формулы приведения к углу, меньшему 90 градусов.

Поэтому, для начала, представим себе угол в 105 градусов как (90 + 15)
Тогда
sin ( 90 + α ) = cos α
sin 105 = sin( 90 + 15 ) = cos 15

cos ( 90 + α ) = - sin α
cos 105 = cos( 90 + 15 ) = -sin 15

tg ( 90 + α ) = -ctg α
tg 105 = tg( 90 + 15 ) = -ctg 15

Примечание. Уже на данном этапе можно посмотреть значения в таблицах синуса, косинуса и тангенса 105 градусов, который преобразован в значения тригонометрических функций синуса, косинуса и тангенса угла 15 градусов. Но, представим себе, что мы тоже их не знаем.

Поэтому, на данном этапе нам на помощь придут формулы преобразования двойного угла тригонометрических функций.
Дело в том, что мы можем представить угол в 30 градусов, как двойной угол 15 градусов ( 2 * 15 ).

Тогда, отталкиваясь от тождества:
cos 2α = 1 - 2sin²α

Принимаем двойной угол как 2 * 15 градусов, тогда
cos 30 = 1 - 2sin²15
sin²15 = ( 1 - cos 30 ) / 2

Значение косинуса для угла 30 градусов легко вычислить. Оно равно √3/2
sin²15 = ( 1 - √3/2 ) / 2
sin 15 = √ (( 1 - √3/2 ) / 2 )

cos 105 = - sin 15
cos 105 = - √ (( 1 - √3/2 ) / 2 )

путем несложных агебраических преобразований получаем:

Синус 105 градусов, косинус 105 градусов, тангенс 105 градусов

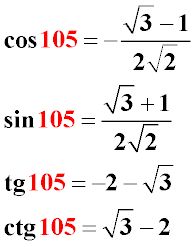
Как видно из примера, значения тригонометрических функций углов синуса, косинуса и тангенса 105 градусов могут быть получены путем несложных тригонометрических преобразований с использованием тригонометрических тождеств преобразований двойных углов и половин заданных углов.

См. также полную таблицу значений тригонометрических функций (таблицу синусов, косинусов и тангенсов).

Ниже приведены также значения тригонометрических функций для угла 105 градусов в виде десятичной дроби с четырьмя знаками после запятой.

5π/12	синус 105 sin 105	косинус 105 cos 105	тангенс 105 tg 105	котангенс 105 ctg 105
Значение	0,9659	-0,2588	-3,7321	-0,2679

Синус, косинус, тангенс угла 30 и 60 градусов (sin cos tg 30 и 60) | Описание курса | Синус, ко синус, тангенс угла 120 градусов (sin 120 cos 120 tg 120)