По условию задачи a = 7 см
Так как площадь грани призмы в данном случае будет равна 7h, где h - высота бокового ребра, количество граней - три, то

49√3 / 4 = 3 * 7h
49√3 / 4 = 21h
откуда
h = 7√3 / 12

Ответ: длина бокового ребра правильной треугольной призмы равна 7√3 / 12

Задача.
Высота правильной треугольной призмы равна h.
Найдите объем призмы, если диагонали боковых граней, не исходящие из одной точки, перпендикулярны.

Решение.
Поскольку в основании призмы по условию лежит правильный треугольник, то все боковые грани в основании равны. Поскольку диагонали каждой из них пересекаются под прямым углом, то боковые грани представляют собой квадрат. Докажем это.


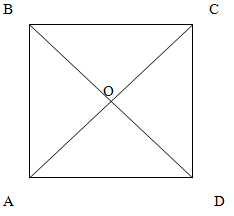
Поскольку AD = BC как основания прямой призмы, углы BOC = AOD как вертикальные, а BCO = OAD, OBC = ODA как внутренние накрест лежащие при параллельных прямых AD и BC. То есть треугольники BOC и AOD  равны.

Отсюда следует, что BO = OD, значит треугольники BOC  и COD также равны, у них смежная сторона OC, а углы COB = COD = 90 градусам. Из этого следует, что CD =BC = AD = AB.

ABCD - квадрат

Следовательно, объем призмы будет равен
V = Sh

Площадь основания - правильный треугольник. Откуда
S = √3/4 h²
V = √3/4 h³

Ответ: √3/4 h³ .