Площадь сферы

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о сфере). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом на форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".

Задача

В сферу вписан конус, образующая которого равна l, а угол при вершине осевого сечения равен 60 градусов. Найдите площадь сферы.

Решение.
Площадь сферы найдем по формуле:

S = 4πr²

Поскольку в сферу вписан конус, проведем сечение через вершину конуса, которое будет равнобедренным треугольником. Поскольку угол при вершине осевого сечения равен 60 градусам, то треугольник - равносторонний (сумма углов треугольника - 180 градусов, значит остальные углы ( 180-60 ) / 2 = 60 , то есть все углы равны ).

Откуда радиус сферы равен радиусу окружности, описанного вокруг равностороннего треугольника. Сторона треугольника по условию равна l . То есть

R = √3/3 l

Таким образом площадь сферы

S = 4π(√3/3 l)²
S = 4/3πl²

Ответ: площадь сферы равна 4/3πl².

Задача

Емкость имеет форму полусферы (полушара). Длина окружности основания равна 46 см. На 1 квадратный метр расходуется 300 граммов краски. Сколько необходимо краски, чтобы покрасить емкость?

Решение.
Площадь поверхности фигуры будет равна половине площади сферы и площади сечения сферы.
Поскольку нам известна длина окружности основания, найдем ее радиус:
L = 2πR
Откуда
R = L / 2π
R = 46 / 2π
R = 23 / π

Откуда площадь основания равна
S = πR²
S = π (23/π) ²
S = 529 / π

Площадь сферы найдем по формуле:
S = 4πr²

Соответственно площадь полусферы
S = 4πr² / 2
S = 2π (23/π) ²
S = 1058 / π

Общая площадь поверхности фигуры равна:
529 / π + 1058 / π = 1587 / π

Теперь вычислим расход краски (учтем, что расход дан на квадратный метр, а вычисленное значение в квадратных сантиметрах, то есть в одном метре 10 000 квадратных сантиметров)
1587 / π * 300 / 10 000 = 47,61 / π граммов ≈ 15,15 г

Задача

Поверхности двух шаров относятся как m:n. Как относятся их объемы?

Поверхні двох куль відносяться як m:n. Як відносяться їх об'єми?

Решение. Рiшення.

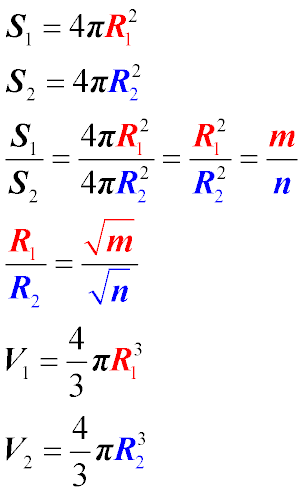	Для пояснения решения прокомментируем каждую из приведенных формул Воспользуемся формулой нахождения поверхности шара и запишем ее для первого шара, предположив, что его радиус равен R₁ Площадь поверхности второго шара запишем с помощью точно такой же формулы, предположив, что его радиус равен R₂ Найдем соотношение их площадей, разделив первое выражение на второе. Сократим полученную дробь. Нетрудно заметить, что соотношение площадей двух шаров равно соотношению квадратов их радиусов. По условию задачи это соотношение равно m/n Из полученного равенства найдем соотношение радиусов шаров путем извлечения квадратного корня. Полученное равенство запомним Воспользуемся формулой нахождения объема шара и запишем ее для первого шара с радиусом R₁ Объем второго шара запишем с помощью той же самой формулы, подставив в нее радиус R₂	Для пояснення рішення прокоментуємо кожну з приведених формул Скористаємося формулою знаходження поверхні кулі і запишемо її для першої кулі, передбачивши, що його радіус рівний R₁ Площу поверхні другої кулі запишемо за допомогою точний такої ж формули, передбачивши, що його радіус рівний R₂ Знайдемо співвідношення їх площ, розділивши перше вираження на друге. Скоротимо отриманий дріб. Неважко відмітити, що співвідношення площ двох куль дорівнює співвідношенню квадратів їх радіусів. По умові завдання це співвідношення рівне m/n З отриманої рівності знайдемо співвідношення радіусів куль шляхом витягання квадратного кореня. Отриману рівність запам'ятаємо Скористаємося формулою знаходження об'єму кулі і запишемо її для першої кулі з радіусом R₁ Об'єм другої кулі запишемо за допомогою тієї ж самої формули, підставивши в неї радіус R₂
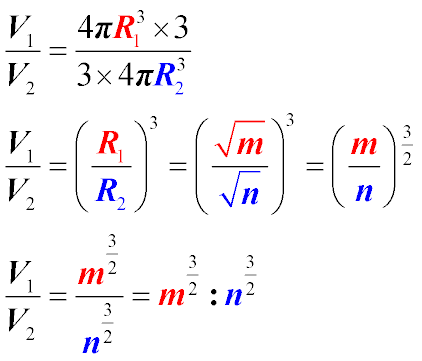	8. Разделим объемы первого и второго шара друг на друга 9. Сократим получившуюся дробь. Заметим, что соотношение объема двух шаров равно соотношению кубов их радиусов. Учтем выражение, полученное нами ранее в формуле 4 и подставим его. Поскольку корень квадратный - это число в степени 1/2, преобразуем выражение 10. Раскроем скобки и запишем полученное соотношение в виде пропорции. Ответ получен.	8. Розділимо об'єми першої і другої кулі один на одного 9. Скоротимо дріб, що вийшов. Відмітимо, що співвідношення об'єму двох куль дорівнює співвідношенню кубів їх радіусів. Врахуємо вираження, отримане нами раніше у формулі 4 і підставимо його. Оскільки корінь квадратний - це число в мірі 1/2, перетворимо вираження 10. Розкриємо дужки і запишемо отримане співвідношення у вигляді пропорції. Відповідь отримана.

Сфера (Шар) | Описание курса | Полусфера