|
Теорема косинусов формулируется следующим образом: квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
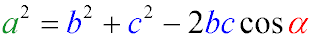
Задача
Одна из сторон треугольника больше другой на 8 сантиметров, а угол между ними равен 120 градусам. Найдите периметр треугольника, если длин третьей стороны равна 28 см.
Решение.
Обозначим одну из сторон треугольника как x, тогда величина другой равна x+8 см.
Исходя из теоремы косинусов, получим:
282 = x2 + (x+8)2-2x(x+8)cos120o
784 = x2 + x2 +16x + 64 - 2x(x+8)(-0,5)
784 = 2x2+16x + 64 + x(x+8)
720 = 3x2 + 16x + 8x
3x2 + 24x +720 = 0
D=9216
x1=((-24)+96)/6=12 (второй корень является отрицательным числом и не имеет смысла в рамках решения задачи)
Таким образом, периметр треугольника P=12+(12+8)+28 = 60 см.
Ответ: 60 см
Задача
В треугольнике АВС сторона АС равна 7√3 см, сторона ВС равна 1 см. Угол С равен 150 градусам. Найти длину стороны АВ.
Решение.
Применим теорему косинусов и соответствующую формулу (см.выше)
AB2 = (7√3)2 + 12 - 2 (7√3) cos 150º
Значение косинуса 150 градусов найдем по таблице значений тригонометрических функций.
AB2 = 147 + 1 - 14√3 (-√3/2)
AB2 = 148 + 21 = 169
AB = 13
Ответ: 13 см
Теорема косинусов и ее доказательство |
Описание курса
| Тангенс и его свойства
|

