|
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия). Если Вам необходимо решить задачу по геометрии,
которой здесь нет - пишите об этом в форуме.
Задача. Осевое сечение цилиндра - квадрат, диагональ которого равна 4 см. Найдите объем цилиндра
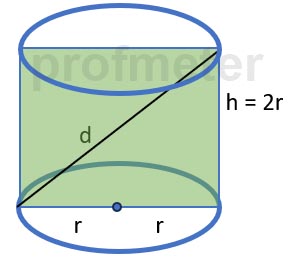
Чтобы решить эту задачу, давайте разберем её по шагам:
- Найти длину стороны квадратного сечения:
-
Диагональ квадрата равна 4 см.
-
Для квадрата соотношение между длиной стороны a и диагональю d определяется формулой:
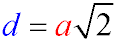
a = d / √2 = 4 / √2 = 2√2 см
-
Определить радиус цилиндра:
-
Длина стороны квадрата равна диаметру основания цилиндра.
-
Следовательно, радиус rr цилиндра:
r = a / 2 = 2√2 / 2 = √2 см
- Найти высоту цилиндра:
-
Высота h цилиндра равна длине стороны квадратного сечения (стороне квадрата):
h=2√2 см
- Вычислить объем цилиндра:
-
Объем V цилиндра определяется формулой:

V=π(√2)2(2√2)=π(2)(2√2)=4√2π см3
Таким образом, объем цилиндра составляет 4√2π см3.
Задача.
Найдите площадь полной поверхности цилиндра, если диагональ его осевого сечения, равная 8см,
составляет с образующей цилиндра угол величиной 30 градусов.
Решение.
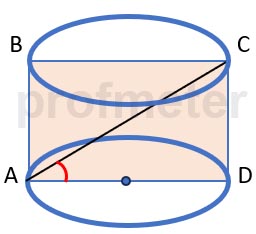
Поскольку AC = 8 см, а угол ACD = 30°, то
CD = AC cos 30°
Пояснение. Треугольник ACD - прямоугольный. Соответственно, CD / AC = cos ∠ACD по свойству тригонометрических функций
в прямоугольном треугольнике. Значение cos 30 найдем из таблицы значений тригонометрических функций.
CD = 8 * √3/2 = 4√3
Аналогично,
AD = AC sin 30°
AD = 8 * 1/2 = 4
Откуда радиус основания цилиндра равен 4/2 = 2 см
Площадь основания цилиндра, соответственно, равна
S1 = πR2 = 4π
Площадь боковой поверхности цилиндра равна площади его развертки - произведению длины окружности основания и высоты цилиндра.
То есть:
S2 = 2πRh = 2π * 2 * 4√3 = 16π√3
Общая площадь поверхности цилиндра равна:
S1 + S2 = 4π + 16π√3
Ответ: 4π + 16π√3
Цилиндр и его сечения (квадрат и вписанный куб) |
Описание курса
| Площадь поверхности цилиндра
|

