|
|
Тригонометрические соотношения (функции) в прямоугольном треугольнике
Соотношения сторон треугольника является основой тригонометрии и геометрии. Большинство задач сводится к использованию свойств треугольников и окружностей, а также прямых. Рассмотрим, что такое тригонометрические соотношения простым языком.
Тригонометрическими соотношениями в прямоугольном треугольнике называются соотношения длин его сторон. При этом такое соотношение всегда одно и то же по отношению к углу, который лежит между сторонами, соотношение между которыми должно быть вычислено.
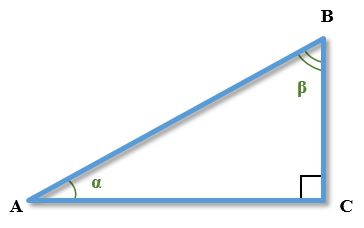
На рисунке обозначен прямоугольный треугольник ABC.
Рассмотрим тригонометрические соотношения его сторон относительно угла A (на рисунке он также обозначен греческой буквой α).
Примем во внимание, что сторона AB треугольника является его гипотенузой. Сторона AC является катетом, прилежащим к углу α, а сторона BC является катетом, противолежащим углу α.
Относительно угла α в прямоугольном треугольнике существуют следующие соотношения:
Косинусом угла называется отношение прилежащего к нему катета к гипотенузе данного прямоугольного треугольника. (см. что такое косинус и его свойства).
На рисунке косинусом угла α является соотношение cos α = AC/AB (прилежащий катет делить на гипотенузу).
Обратите внимание, что для угла β прилежащим катетом является уже сторона BC, поэтому cos β = BC / AB. То есть тригонометрические соотношения вычисляются в соответствии с положением сторон прямоугольного треугольника относительно угла.
При этом буквенные обозначения могут быть любыми. Важно лишь взаимное расположение угла и сторон прямоугольного треугольника.
Синусом угла называется соотношение противолежащего к нему катета к гипотенузе прямоугольного треугольника (см. что такое синус и его свойства).
На рисунке синусом угла α является соотношение sin α = BC / AB (противолежащий катет делить на гипотенузу).
Поскольку для определения синуса важны взаимное расположение сторон прямоугольного треугольника относительно заданного угла, то для угла β функция синуса будет sin β = AC / AB.
Тангенсом угла называется соотношение противолежащего данному углу катета к прилежащему катету прямоугольного треугольника (см. что такое тангенс и его свойства ).
На рисунке тангенс угла α будет равен соотношению tg α = BC / AC. (противолежащий углу катет делить на прилежащий катет)
Для угла β, руководствуясь принципов взаимного расположения сторон, тангенс угла можно будет вычислить как tg β = AC / BC.
Котангенсом угла называется соотношение прилежащего данному углу катета на противолежащий катет прямоугольного треугольника. Как видно из определения, котангенс - эта функция, связанная с тангенсом соотношением 1/tg α . То есть они взаимно обратные.
Задача. Найти тригонометрические соотношения в треугольнике
В треугольнике АВС угол С равен 90 градусам. cos α = 4/5. Надите sin α, sin β
Решение.
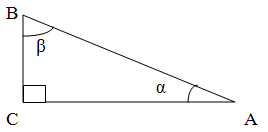
Поскольку cos α = 4/5, то AC / AB = 4 / 5. То есть стороны соотносятся как 4:5. Обозначим длину AC как 4x, тогда AB = 5x.
По теореме Пифагора:
BC2 + AC2 = AB2
Тогда
BC2 + ( 4х )2 = ( 5х )2
BC2 + 16х2 = 25х2
BC2 = 9х2
BC = 3x
sin α = BC / AB = 3x / 5x = 3/5
sin β = AC / AB, а его значение и так известно по условию, то есть 4/5
Ответ: 3/5, 4/5
Тангенс и его свойства |
Описание курса
| Тригонометрический круг
|

