Призма с треугольником в основании ( часть 2)

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о призме). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".

Задача. Правильная треугольная призма

Площадь боковой поверхности правильной треугольной призмы равна площади основания. Вычислите длину бокового ребра, если сторона основания 7см.

Решение.

"Подвох" кроется в формулировке задачи - если призма правильная треугольная (см. определение призмы), то в ее основании лежит правильный треугольник.

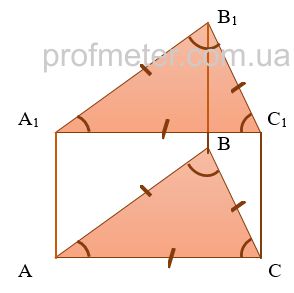
Правильная треугольная призма, в основании которой лежит правильный треугольник. Все стороны основания равны, углы треугольника в основании равны

Правильная треугольная призма, в основании которой лежит правильный треугольник. Все стороны основания равны, углы треугольника в основании равны

Площадь правильного треугольника, который является основанием правильной треугольной призмы, найдем по формуле:
S = a²√3 / 4
S = 49√3 / 4

Площадь боковой поверхности правильной треугольной призмы найдем по формуле
S = 3 ab
тогда
S = 3 * 7 * b = 21b

Таким образом,
49√3 / 4 = 21b
b = 49√3 / 84
b = 7√3 / 12

Ответ: 7√3 / 12

Задача. Прямоугольный треугольник в основании прямой призмы

В основании прямой треугольной призмы лежит прямоугольный треугольник с катетами 8 и 6 см. Найти боковое ребро призмы, если ее боковая поверхность равна 120 квадратных сантиметров.
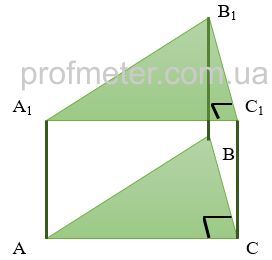
Прямая призма ABCA1B1C1 с прямоугольным треугольником в основании

Прямая призма ABCA1B1C1 с прямоугольным треугольником в основании

Решение.
Сначала найдем гипотенузу основания призмы. Поскольку в основании призмы лежит прямоугольный треугольник, воспользуемся теоремой Пифагора.
(см. свойства и формулы прямоугольного треугольника)

AB² = AC² + BC²
AB² = 8² + 6²
AB² = 64 + 36
AB = √100
AB = 10

Обозначим боковое ребро призмы как h . Боковое ребро одновременно является и высотой призмы, поскольку по условию задачи призма является прямой.
(см. свойства призмы)
Тогда площадь боковой поверхности призмы является суммой площадей трех прямоугольников - ACC1A1, CBB1C1 и ABB1A1 или, если подставить известные значения катетов основания призмы, то

10h + 6h + 8h = 120
24h = 120
h =5

Ответ: ребро прямоугольной призмы с прямоугольным треугольником в основании равно 5 см.

Призма с правильным треугольником в основании (часть 2) | Описание курса | Призма с треугольником в основании ( часть 3)