Описание курса Аксиомы планиметрии Аксиома принадлежности точек и прямых Аксиома расположения точек на прямой Аксиома про длину отрезков Аксиома расположения точек относительно прямой Аксиома свойств измерения углов Аксиома свойств откладывания отрезков Аксиома свойств откладывания углов Существование треугольника, равного данному Свойство параллельных прямых Точки, отрезки и прямые Геометрическое место точек. Метод геометрических мест Отрезки в координатной плоскости Прямые на координатной плоскости Пересекающиеся прямые Луч Векторы Центральная и осевая симметрия Угол. Углы на плоскости Вертикальные и смежные углы Биссектриса угла Биссектриса углов треугольника Биссектриса внешнего угла Биссектриса. Примеры решения задач Площадь геометрической фигуры Окружность. Уравнение окружности Задачи про окружность Хорда Треугольник (Трикутник) Высота треугольника Сумма углов треугольника Площадь треугольника Медиана треугольника Как найти длину медианы треугольника Нахождение площади через медианы Угол между высотой и медианой треугольника Медиана прямоугольного треугольника Медіана прямокутного трикутника Подобие треугольников Простейшие задачи на подобие треугольников Подобие треугольников. Первый признак подобия Подобие треугольников. Третий признак подобия Подобие треугольников. Использование в задачах Прямоугольный треугольник Прямоугольный треугольник Биссектриса в прямоугольном треугольнике Высота в прямоугольном треугольнике Высота в прямоугольном треугольнике (Часть 2) Теорема Пифагора и ее доказательство Применение теоремы Пифагора Гипотенуза прямоугольного треугольника Перпендикуляр к плоскости прямоугольного треугольника Равнобедренный треугольник Равнобедренный треугольник Рівнобедрений трикутник Площадь равнобедренного треугольника Площа рівнобедреного трикутника Углы равнобедренного треугольника Высота равнобедренного треугольника Окружность, вписанная в равнобедренный треугольник Окружность, описанная вокруг треугольника Окружность, описанная вокруг треугольника Окружность, описанная вокруг треугольника (часть 2) Вписанная в треугольник окружность Четырехугольник Существование четырехугольника Периметр четырехугольника Окружности, вписанные и описанные вокруг четырехугольника Углы четырехугольника Правильный четырехугольник (квадрат). Правильний чотирикутник (квадрат) Ромб Трапеция Площадь трапеции Высота трапеции Трапеция (задачи про основания) Диагонали трапеции Прямоугольная трапеция Равнобокая (равнобедренная) трапеция Углы равнобокой (равнобедренной) трапеции Высота равнобедренной трапеции Равнобокая трапеция Равнобокая трапеция (часть 2) Трапеция, описанная вокруг окружности Параллелограмм Параллелограмм. Задачи про площадь и стороны Параллелограмм (часть 2) Площадь параллелограмма Высота параллелограмма Прямоугольник Периметр прямоугольника Периметр и площадь прямоугольника Тригонометрия Синус Теорема синусов Задачи на решение с помощью теоремы синусов Теорема синусов (часть 2) Косинус Основное свойство функции косинуса Теорема косинусов и ее доказательство. Теорема косинусов. Пример решения задачи Тангенс и его свойства Тригонометрические соотношения в прямоугольном треугольнике Тригонометрический круг Радианы и градусы. Радiани i градуси Таблица значений тригонометрических функций Синус, ко синус, тангенс угла 15 градусов (sin 15 cos 15 tg 15) Синус, косинус и тангенс угла 30 градусов (sin cos tg 30) - таблица значений Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45) Синус, косинус, тангенс угла 30 и 60 градусов (sin cos tg 30 и 60) Синус, косинус, тангенс угла 105 градусов (sin 105 cos 105 tg 105) Синус, ко синус, тангенс угла 120 градусов (sin 120 cos 120 tg 120) Тригонометрические тождества и преобразования Пояснение (доказательство) простейших тригонометрических тождеств Преобразования тригонометрических функций вида (α + a/bπ) и доказательство Тригонометрические формулы понижения степени sin cos tg Косинус двойного угла Многоугольники Правильный многоугольник Шестиугольник и его свойства Сумма углов многоугольника Стереометрия Прямые и плоскости Параллельность плоскостей. Свойства и признаки параллельности. Параллельные плоскости Перпендикулярные плоскости Прямые на плоскости Точка и плоскость Отрезок, пересекающий плоскость Наклонная из точки к плоскости Параллелограмм, рассеченный плоскостью Параллелограмм и плоскость Перпендикуляр к квадрату Перпендикуляр к плоскости прямоугольного треугольника Призма. Параллелепипед. Куб. Решение задач Объем призмы Площадь боковой поверхности призмы Прямая призма Правильная четырехугольная призма Куб Диагональное сечение правильной призмы Параллепипед Площадь поверхности и объем параллелепипеда Призма с треугольником в основании Призма с правильным треугольником в основании Призма с правильным треугольником в основании (часть 2) Призма с треугольником в основании ( часть 2) Призма с треугольником в основании ( часть 3) Параллелограмм в основании призмы Ромб в основании призмы Пирамида. Решение задач С треугольником в основании Тетраэдр (пирамида) Пирамида с прямоугольным треугольником в основании Пирамида с равнобедренным треугольником в основании Правильная треугольная пирамида (правильная пирамида с треугольником в основании). Тетраэдр Периметр основания правильной треугольной пирамиды Объем правильной треугольной пирамиды Площадь поверхности правильной треугольной пирамиды Площадь боковой поверхности правильной треугольной пирамиды Правильный тетраэдр (пирамида) Пирамида и вписанный конус Правильная пирамида Апофема правильной пирамиды Объем правильной усеченной пирамиды Правильная пирамида с четырехугольником в основании Правильная пирамида с четырехугольником в основании Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании Правильная пирамида с четырехугольником в основании (часть 3) Нахождение углов пирамиды Нахождение величины наклона боковых граней правильной прамиды Нахождение расстояний в правильной четырехугольной пирамиде С четырехугольником в основании Пирамида Неправильная пирамида с прямоугольником в основании Неправильная пирамида с четырехугольником в основании Сфера. Шар. Куля Сфера (Шар) Площадь сферы Полусфера Соотношение объема шара и конуса Цилиндр Задачи про цилиндр со вписанной призмой Цилиндр и его сечения Цилиндр и его сечения (квадрат и вписанный куб) Диагональ цилиндра Площадь поверхности цилиндра Конус Конус Площадь боковой поверхности конуса Объем конуса Объем конуса (2)

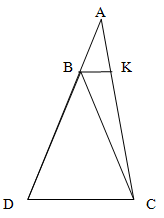
Примечание. В данном уроке изложены задачи по геометрии о биссектрисе. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Почти наверняка курс будет дополнен. Задача. На стороне AD треугольника ADC отмечена точка B так,что BC = BD. Докажите,что прямая DC параллельна биссектрисе угла ABC. Решение. Поскольку по условию задачи BC = BD, то треугольник DBC - равнобедренный. Для данного треугольника угол CBA является внешним. Таким образом, решение задачи сводится к доказательству утверждения, что биссектриса внешнего угла равнобедренного треугольника параллельна его основанию. Угол DBA - равзвернутый и равен 180 градусам. Сумма углов треугольника также DBC равна 180 градусам. Поскольку в состав развернутого угла DBA входит угол DBC, то градусная мера угла ABC равна сумме остальных углов равнобедренного треугольника, которые равны между собой. Таким образом, угол ABC равен удвоенной градусной мере угла DCB. Исходя из того, что BK - биссектриса угла ABC, то углы KBC = DCB. Рассмотрим прямые BK и DC. Их внутренние накрест лежащие углы равны (KBC = DCB). Таким образом, прямые параллельны. 0    Биссектриса углов треугольника | Описание курса | Биссектриса. Примеры решения задач

Обсудить на форуме
Записаться на курсы
Обратиться к консультанту
Пройти тест
Полный список курсов обучения
Бесплатные видеоуроки
Нужна информация!