Рівнобедрений трикутник
Визначення рівнобедреного трикутника
Рівнобедрений трикутник - це трикутник, в якому довжини двох його сторін рівні між собою..
Примітка. З визначення рівнобедреного трикутника випливає, що правильний трикутник також є рівнобедреним. Однак, необхідно пам'ятати, що зворотне твердження - невірно.
Властивості рівнобедреного трикутника
Властивості, наведені нижче, використовуються при вирішенні завдань. Оскільки вони широко відомі, то мається на увазі, що вони не потребують пояснення. Тому в текстах завдань посилання на них опущені.
- Кути, протилежні рівним сторонам рівнобедреного трикутника, рівні між собою.
-
Бісектриси, медіани і висоти, проведені з кутів, протилежних рівним сторонам трикутника, рівні між собою.
- Бісектриса, медіана і висота, проведені до основи, збігаються між собою.
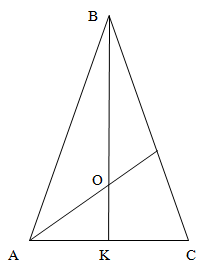
- Центри вписаного і описаного кіл лежать на висоті, бісектрисі і медіані (вони збігаються) проведених до основи.
- Кути, протилежні рівним сторонам рівнобедреного трикутника, завжди гострі.
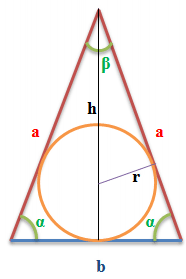
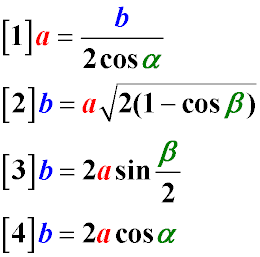Сторони в трикутнику можуть бути обчислені за допомогою формул, що виражають їх довжину через інші сторони і кути, величина яких відома.
Бічна сторона рівнобедреного трикутника дорівнює частці від ділення основи на подвійний косинус кута при основі (Формула 1). Дана тотожність може бути отримана шляхом нескладних перетворень з теореми косинусів.
Основа рівнобедреного трикутника дорівнює добутку бічної сторони на квадратний корінь з подвоєної різниці одиниці і косинусу кута при вершині (Формула 2).
Основа рівнобедреного трикутника дорівнює подвоєному добутку бічної сторони на синус половини кута при вершині. (Формула 3).
Основа рівнобедреного трикутника дорівнює подвоєному добутку бічної сторони на косинус кута при його основі (Формула 4).
Радіус вписаного кола в трикутник
|
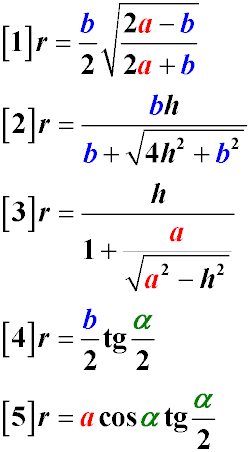
Позначення в формулах, можна подивитися на малюнку вище.
Радіус вписаного кола для рівнобедреного трикутника можна знайти, виходячи з величин основи і кожного боку. (Формула 1).
Радіус вписаного кола для рівнобедреного трикутника можна визначити, виходячи з величин основи і висоти, проведеної до цієї основи (Формула 2).
Радіус вписаного в трикутник кола можна також обчислити через довжину бічної сторони і висоту, проведену до основи трикутника (Формула 3).
Знання величини кута між бічними сторонами і довжини основи також дозволяє визначити радіус вписаного кола (Формула 4).
Аналогічна Формула 5 дозволяє визначити радіус вписаного кола через бічні сторони і кут між ними.
|
Ознаки рівнобедреного трикутника
Трикутник, у якого присутні перераховані нижче ознаки, є рівнобедреним:
- Два кути трикутника рівні;
- Висота збігається з медіаною;
- Висота збігається з бісектрисою;
- Бісектриса збігається з медіаною;
- Дві висоти рівні;
- Дві медіани рівні;
- Дві бісектриси рівні.
Площа рівнобедреного трикутника
Площа рівнобедреного трикутника знаходиться за наступними формулами:
,
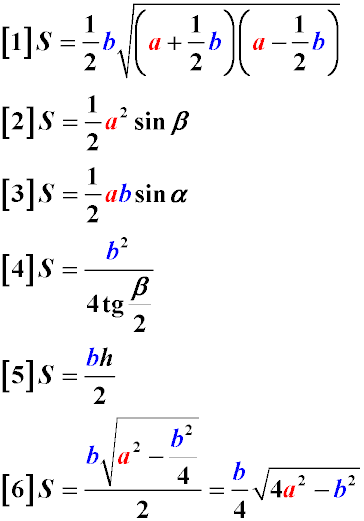де
a - довжина однієї з двох рівних сторін трикутника;
b - довжина основи;
α - величина одного з двох рівних кутів при основі;
β - величина кута між рівними сторонами трикутника і протилежної йому основи..
См. також "Площа трикутника".
