|
Примечание: см. также таблицу значений тригонометрических функций других углов.
Синус, косинус, тангенс угла 45 градусов (sin 45, cos 45, tg 45)
Табличные значения синуса 45, косинуса 45 и тангенса 45 градусов указаны ниже.
Далее по тексту следует пояснение метода и правильности вычисления этих значений для произвольного прямоугольного треугольника.
45 градусов - это π/4 радиан. Формулы для значений косинуса, синуса и тангенса пи/4 радиан указаны ниже (хотя они и тождественны).
То есть, например, tg π/4 = tg 45 градусов
ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ПРИ α=45°
Как самостоятельно вычислить значения sin cos tg 45 градусов?
Построим и рассмотрим прямоугольный треугольник АВС у которого угол ∠В = 45°. На основании соотношения его сторон,
вычислим значения тригонометрических функций в прямоугольном треугольнике для угла 45 градусов. Поскольку треугольник прямоугольный,
то значения функций синуса, косинуса и тангенса будут равны соотношению его соответствующих сторон.
Поскольку значение функций синуса, косинуса и тангенса зависят исключительно от градусной меры угла (или значения, выраженного в радианах),
то найденные нами соотношения и будут значениями функции синуса 45, косинуса 45 и тангенса 45 градусов.
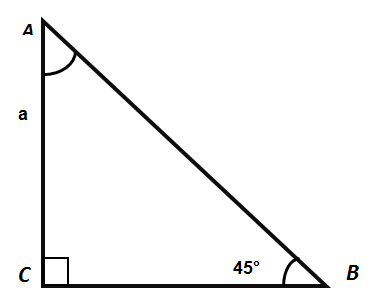
Согласно свойствам прямоугольного треугольника, угол С - прямой и равен 90 градусам.
Угол B мы изначально построили с градусной мерой 45 градусов. Найдем значение угла А. Так как сумма углов треугольника равна 180 градусам, то
∠А + ∠В + ∠С = 180°
Угол C прямой и равен 90 градусам, угол B мы изначально определили как 45 градусов, таким образом:
∠А = 180° -∠С - ∠В = 180° - 90° - 45° = 45°
Поскольку у данного треугольника два угла равны между собой, то треугольник АВС – прямоугольный, и, одновременно, равнобедренный,
в котором оба катета равны между собой: AC = BC.
Допустим, что длина сторон равна некому числу АС = ВС = а. Зная длины катетов, вычислим длину гипотенузы.
По теореме Пифагора: АВ2=АС2+ВС2
Заменим длины AC и BC на переменную а, тогда получим:
АВ2 = а2 + а2 = 2а2,
тогда АВ=а√2.
В результате мы выразили длины всех сторон прямоугольного треугольника с углом 45 градусов через переменную а.
Согласно свойств тригонометрических функций в прямоугольном треугольнике соотношение соответствующих сторон треугольника
будет равным значению соответствующих функций. Таким образом для угла α = 45 градусов:
sin α = BC / AB (согласно определению синуса для прямоугольного треугольника - это отношение противолежащего катета к гипотенузе,
BC - катет, AB - гипотенуза)
cos α = AC / AB (согласно определению косинуса - это отношение прилежащего катета к гипотенузе, AC - катет, AB - гипотенуза)
tg α = BC / AC (аналогично, тангенс для угла α будет равен отношению противолежащего катета к прилежащему)
Вместо обозначений сторон подставим значения их длин через переменную а.
Исходя из этого (см. таблицу значений sin 45, cos 45, tg 45) получаем:
Табличные значения sin 45, cos 45, tg 45 (то есть значение синуса 45, косинуса 45 и тангенса 45 градусов можно вычислить
как соотношение соответствующих сторон данного треугольника), подставим вычисленные выше значения длин сторон в формулы
и получим результат на картинке ниже.
Табличные значения: синус 45, косинус 45 и тангенс 45 градусов
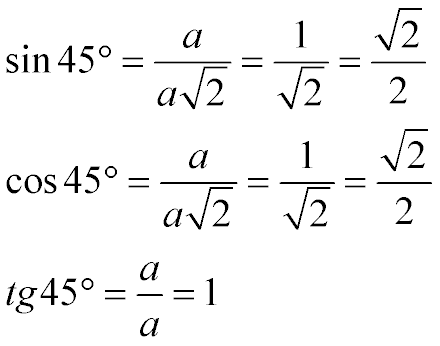
Таким образом:
- тангенс 45 градусов равен единице
- синус 45 градусов равен косинусу 45 градусов и равен корню из двух пополам (то же самое, что и единица, деленная на корень из двух)
Как видно из вычислений, приведенных выше, для вычисления значений соответствующей тригонометрической функции важны не длины
сторон треугольника, а их соотношение, которое всегда одно и то же для одинаковых углов, независимо от размеров конкретного треугольника.
Синус, косинус и тангенс угла π/4 радиан
В задачах, предлагаемых для решения в старших классах и на ЗНО/ЕГЭ вместо градусной меры угла часто встречается указание на его величину,
измеренную в радианах. Мера угла, выраженная в радианах, базируется на числе пи, которое выражает зависимость длины окружности
от ее диаметра.
Для простоты понимания, рекомендую запомнить простой принцип перевода градусов в радианы. Диаметр окружности охватывает дугу,
равную 180 градусам. Таким образом, пи радиан будет равно 180 градусам. Откуда легко пересчитать любую градусную меру угла в радианы
и обратно.
Учтем, что угол 45 градусов, выраженный в радианах, равен (180 / 45 = 4) π/4 ( пи на четыре). Поэтому найденные нами значения верны
для той же самой градусной меры угла, выраженной в радианах:
- тангенс π/4 ( пи на четыре) равен единице
- синус π/4 ( пи на четыре) градусов равен косинусу π/4 градусов и равен корню из двух пополам
Для удобства зрительного восприятия эти значения приведены на рисунке ниже.
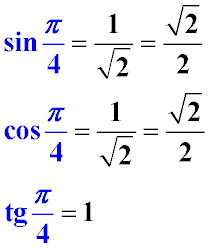
Примечание. В поисковых запросах часто встречается нечто типа "тангенс р/4 или p/4". Это неграмотно. Используйте запрос,
например "тангенс пи/4".
Примечание: см. также таблицу значений тригонометрических функций остальных углов.
Синус, косинус и тангенс угла 30 градусов (sin cos tg 30) - таблица значений |
Описание курса
| Синус, косинус, тангенс угла 30 и 60 градусов (sin cos tg 30 и 60)
|

