|
|
Гипотенуза прямоугольного треугольника
Гипотенуза - это сторона прямоугольного треугольника, противолежащая прямому углу.

На рисунке гипотенуза прямоугольного треугольника обозначена красным цветом.
Свойства гипотенузы
- Гипотенуза является самой длинной стороной прямоугольного треугольника
- Если вокруг прямоугольного треугольника описана окружность, то гипотенуза является диаметром такой окружности, а ее центр делит гипотенузу пополам
Формулы для нахождения длины гипотенузы
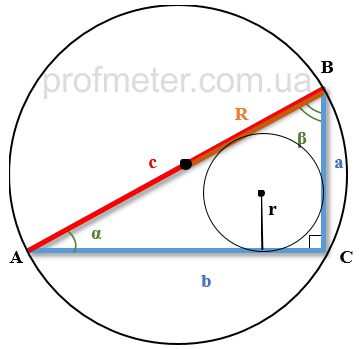
Формулы нахождения длины гипотенузы соответствуют рисунку выше, где:
c - гипотенуза прямоугольного треугольника
a, b - катеты прямоугольного треугольника
α, β - острые углы
R - радиус описанной окружности
r - радиус вписанной окружности
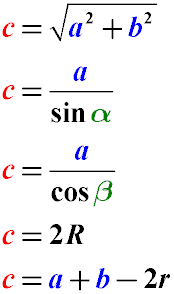
- Длина гипотенузы прямоугольного треугольника равна квадратному корню из суммы квадратов катетов (Теорема Пифагора)
- Длина гипотенузы равна длине катета, деленного на синус противолежащего ему угла
- Длина гипотенузы равна длине катета, деленного на косинус прилежащего к нему угла
- Длина гипотенузы равна двойному радиусу описанной вокруг прямоугольного треугольника окружности
- Длина гипотенузы прямоугольного треугольника равна сумме катетов этого треугольника минус двойной радиус вписанной окружности
Применение теоремы Пифагора |
Описание курса
| Перпендикуляр к плоскости прямоугольного треугольника
|

