|
Примечание. В данном уроке изложены задачи по геометрии о медиане треугольника. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Почти наверняка курс будет дополнен.
Задача. Найти угол между высотой и медианой прямоугольного треугольника
| Найдіть кут між медіаною і висотою прямокутного трикутника , які проведені з вершини прямого кута , якщо гострий кут дорівнює 20 градусів | Найдите угол между высотой и медианой прямоугольного треугольника, которые проведены из вершины прямого угла, если острый угол равен 20 градусов |
.
Решение.
Решим задачу путем дополнительного построения вокруг заданной геометрической фигуры (треугольника), чтобы использовать свойства новой образованной фигуры (прямоугольника) для решения этой задачи по геометрии
Сначала достроим прямоугольный треугольник до прямоугольника.
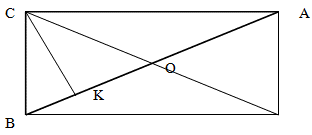
В результате дополнительного построения катеты прямоугольного треугольника одновременно являются сторонами прямоугольника, а гипотенуза - его диагональю.
Далее учтем следующие свойства треугольника и прямоугольника:
- Сумма углов треугольника равна 180 градусам
- Диагонали прямоугольника в точке пересечения делятся пополам
- Диагонали прямоугольника равны
Величина одного из углов треугольника задана в условии задачи. Поскольку треугольник по условию прямоугольный, то мы можем найти величину третьего угла, зная, что сумма углов треугольника равна 180 градусам.
Поскольку угол CAB = 20°, то угол ABC = 180 - 90 - 20 = 70°
Таким образом, мы нашли градусную меру угла B в треугольнике ABC
Рассмотрим треугольник COA. Он равнобедренный, так как его стороны - это половины диагоналей прямоугольника. Это следует из свойств прямоугольника. Так как диагонали прямоугольника равны, а в точке пересечения они делятся пополам, то половины равных отрезков будут также между собой равны. Поскольку в равнобедренном треугольнике углы при основании равны, то:
∠OCA = ∠OAC = 20º
Рассмотрим треугольник BKC. CK является высотой треугольника ABC, проведенной к гипотенузе. Значит угол BKC - прямой, то есть равен 90 градусам, а сам треугольник BKC - прямоугольный. Поскольку треугольник BKC - прямоугольный, то угол BCK = 180 - 90 - 70 = 20°. (Это следует из того, что сумма углов треугольника 180 градусов, угол BKC - прямой, а величину угла B мы нашли ранее)
Поскольку угол BCA - прямой, то его градусная мера равна 90 градусов и, одновременно, равна сумме градусных мер составляющих его углов: BCK, KCO и OCA.
Величину угла BCK мы только что нашли, она составляет 20 градусов, величину угла OCA мы также нашли ранее и она тоже составляет 20 градусов.
Откуда:
20° + 20° + ∠KCO = 90°
∠KCO = 50°
Ответ: Угол между медианой и биссектрисой заданного прямоугольного треугольника равен 50 градусов.
Нахождение площади через медианы |
Описание курса
| Медиана прямоугольного треугольника
|

