МЕДИАНА ТРЕУГОЛЬНИКА
Слово «медиана» переводится как «равноделящая сторону». Чтобы построить медиану, надо середину стороны треугольника соединить отрезком с противолежащей вершиной треугольника. Полученный отрезок и есть медиана треугольника.
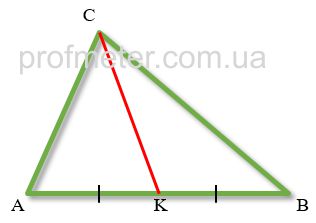
Медиана треугольника – отрезок, проведенный из вершины треугольника, соединяющий эту вершину с серединой противолежащей стороны треугольника.
На рисунке красным цветом обозначена медиана CK. При этом она делит сторону AB треугольника пополам, AK = KB.
Свойства медианы треугольника
Все медианы треугольника пересекаются в одной точке, расположенной в плоскости треугольника и являющейся его центром тяжести.
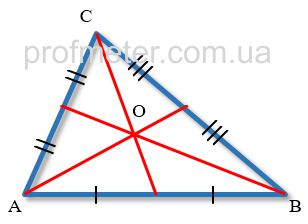
Для определения этой точки достаточно построить две медианы треугольника, и точка их пересечения будет принадлежать третьей медиане этого треугольника.
-
Точкой пересечения медиан треугольника каждая медиана делится в отношении 2:1, считая от вершины треугольника. Т.е. длина отрезка медианы от вершины треугольника до точки пересечения медиан составляет 2/3 всей ее длины, а от точки пересечения медиан до стороны треугольника - 1/3 ее длины.
-
Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
-
Треугольник делится тремя медианами на шесть равновеликих треугольников.
-
Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
-
В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
-
Большей стороне треугольника соответствует меньшая медиана.
-
У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают.
-
У равностороннего треугольника все три «замечательные» линии (высота, биссектриса и медиана) совпадают и три «замечательных» точки (точки ортоцентра, центра тяжести и центра вписанной и описанной окружностей) находятся в одной точке пересечения «замечательных» линий, т.е. тоже совпадают.
Средняя линия треугольника
Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией.
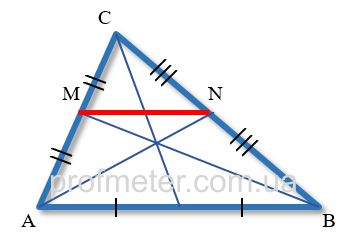
Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.
Формулы медианы произвольного треугольника
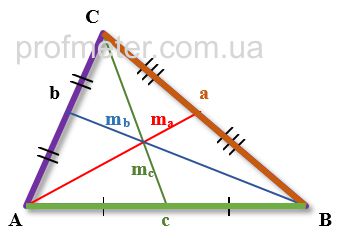
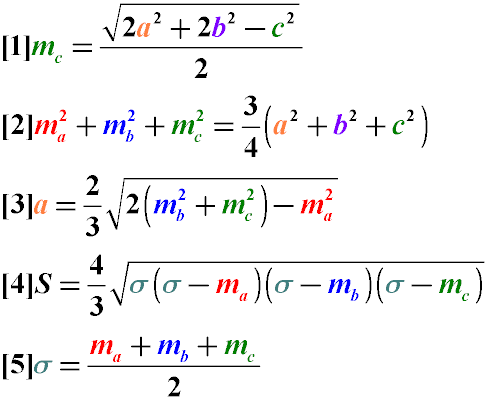
- Длина медианы, проведенной к стороне произвольного треугольника равна половине квадратного корня из удвоенной суммы квадратов двух других сторон из которой вычтен квадрат стороны, к которой проведена медиана (Формула 1)
- Сумма квадратов медиан треугольника равна 3/4 суммы квадратов его сторон (Формула 2)
- Длина стороны треугольника равна 2/3 квадратного корня из удвоенной суммы квадратов медиан, проведенных к двум другим его сторонам за вычетом квадрата медианы, проведенной к искомой стороне (Формула 3)
- Площадь треугольника можно найти через длины его медиан, используя значение полусуммы длин медиан (Формулы 4 и 5)
Площадь треугольника |
Описание курса
| Как найти длину медианы треугольника
|

