|
|
Примечание. Это урок с решениями задачам по геометрии (раздел стереометрия, пирамида с четырехугольником в основании).
Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме.
В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня,
а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".
Задача
В правильной четырёхугольной пирамиде сторона основания равна а, высота равна 3а.
Найдите углы наклона боковых рёбер и боковых граней к плоскости основания.
Решение.
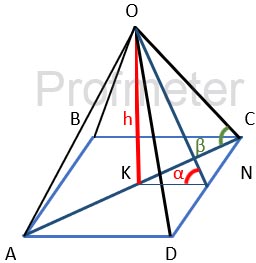
Найдем угол наклона ребер к плоскости основания.
Поскольку в основании правильной пирамиды лежит правильный четырехугольник, то, в данном случае, это - квадрат.
Поскольку высота пирамиды проецируется в центр основания, то это - точка пересечения диагоналей.
Откуда KN = а/2
Треугольник OKN - прямоугольный, OK - высота, равная 3а.
Найдем тангенс угла KNO, обозначив его как α.
tg α = OK / KN
tg α = 3a / (a/2) = 6
α = arctg 6 ≈ 80.5377°
Найдем угол наклона ребра пирамиды.
Диагональ квадрата со стороной а равна а√2. Поскольку высота проецируется в центр основания, то в этой точке
диагонали делятся пополам.
Таким образом, для прямоугольного треугольника OKC тангенс угла KCO (обозначим его как β ) равен
tg β = OK / KC
tg β = 3a / (а√2/2) = 6 / √2
β = arctg 6/√2 ≈ 76.7373°
Ответ: угол наклона граней arctg 6 ≈ 80.5377°; угол наклона ребер arctg 6/√2 ≈ 76.7373°
Правильная пирамида с четырехугольником в основании (часть 3) |
Описание курса
| Нахождение величины наклона боковых граней правильной прамиды
|

