|
Объем любого параллелепипеда равен произведению площади основания на высоту параллелепипеда:
V=Sосн.*H
Объем призмы равен произведению площади ее основания на высоту
Vпризмы=Sосн.*H
Два тела называются равновеликими, если они имеют равные объемы.
Две треугольные пирамиды с равными площадями оснований и равными высотами – равновелики.
Если при сечении двух тел плоскостью, параллельной основанию (или параллельной заданной плоскости), площади сечений одинаковы, то эти тела равновелики – принцип Кавальери.
|
Об'єм будь-якого паралелепіпеда дорівнює добутку площі основи на висоту паралелепіпеда:
V=Sосн.*H
Об'єм призми дорівнює добутку площі її основи на висоту
Vпризмы=Sосн.*H
Два тіла називаються рівновеликими, якщо вони мають рівні об'єми.
Дві трикутні піраміди з рівними площами підстав і рівними висотами - рівновеликі.
Якщо при перетині двох тіл площиною, паралельною до основи (або паралельною заданій площині), площі перерізів однакові, то ці тіла рівновеликі - принцип Кавальєрі.
|
Задача
Основанием параллелепипеда служит квадрат. Одна из вершин его верхнего основания одинаково удалена от всех вершин нижнего основания. Определите высоту параллелепипеда, если диагональ основания равна 8 см, а боковое ребро равно 5 см.
Решение.
Поскольку одна из вершин основания параллелепипеда (обозначим ее F) одинаково удалена от всех вершин нижнего основания параллелепипеда, то вместе с диагональю нижнего основания (обозначим ее AC) она образует равнобедренный треугольник AFC. AF = AC по условию. Одновременно, AF - это ребро параллелепипеда.
Таким образом, в равнобедренном треугольнике AFC стороны равны следующим величинам: AF=FC=5 см , AC = 8 см.
Высота равнобедренного треугольника AFC одновременно, будет являться высотой параллелепипеда. Пусть она опущена в точке K.
Кроме того, высота равнобедренного треугольника делит его основание пополам. Откуда, по теореме Пифагора высота будет равна:
FK
2 + (AC/2)
2 = FC
2
FK
2 + 16 = 25
FK
2 = 9
FK = 3 см
Ответ: высота параллелепипеда равна 3 см.
Задача
Найти площадь основания ABCD прямоугольного параллелепипеда ABCDA1B1C1D1 если DB1 = 6 см, DB = 5 см, BC1 = 4 см.
Решение.
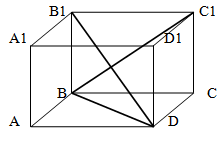
Для нахождения длин сторон ( поскольку параллелепипед в условии задачи прямоугольный, а значит, все ребра пересекаются под прямым углом ) используем теорему Пифагора.
Найдем BB1 в прямоугольном треугольнике DBB1
BB1 = √( B1D2 - BD2 )
BB1 = √(36 - 25) = 3
Соответственно
СС1 = BB1 = 3 см
Для прямоугольного треугольника BC1C
BC = √( BC12 - C1C2 )
BC = √( 16 - 9 ) = √7
В треугольнике BCD найдем CD
CD = √( BD2 - BC2 )
CD = √( 25 - 7 ) = √18 = 3√2
Откуда площадь основания параллелепипеда равна:
S = BC * CD = √7 * 3√2 = 3√14
Ответ: площадь основания прямоугольного параллелепипеда равна 3√14

