|
|
Задача.
Окружность радиусом 4 вписана в равнобедренный треугольник MNK с основанием MK и касается стороны MN в точке С. найдите боковую сторону треугольника, если она в 5 раз больше отрезка CN.
Решение.
Пусть длина отрезка CN = x , тогда MN = 5х . То есть боковая сторона равнобедренного треугольника равна a = 5x
Примем во внимание формулу радиуса окружности для равнобедренного треугольника и формулу нахождения полупериметра равнобедренного треугольника.
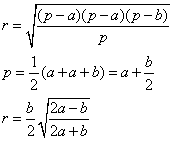
Расстояние от вершины С треугольника до точки, в которой вписанная окружность касается стороны равно
d = p - c
Подставим известные значения
x = a + b/2 - a
x = b/2
Откуда основание равнобедренного треугольника
b = 2x
Подставим значения a и b в формулу радиуса вписанной окружности. Получим
r = x√(2/3)
4 = x√(2/3)
x = 4 / √(2/3)
Откуда a = 5x = 20 / √(2/3)
Ответ: 20 / √(2/3)
Высота равнобедренного треугольника |
Описание курса
| Окружность, описанная вокруг треугольника
|

