Нахождение площади через медианы

Задача.
В треугольнике ABC медианы CD и BE пересекаются в точке К. Найдите площадь четырехугольника ADKE, если BC = 20 см, AC = 12 см,
а угол ACB равен 135 градусам.

Решение.
Кроме медиан, указанных в условии, проведем медиану к третьей стороне треугольника.
Треугольник с медианами

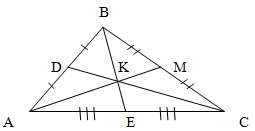
Решим задачу шаг за шагом:

Свойства медиан:
- Медианы треугольника пересекаются в одной точке, которая называется центроидом, и делятся этой точкой на две части
  в отношении 2:1, считая от вершины.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
Площадь треугольника:
- Площадь треугольника можно найти по формуле S=1 / 2 ab sin ⁡γ, где a и b - стороны треугольника, а γ - угол между ними.
- Дано BC = 20 см, AC = 12 см, и ∠ACB=135°:

S =1 / 2 × 20 × 12 × sin⁡135°

Значение синуса 135 градусов: sin⁡135°= √2 / 2

S=1/2×20×12×√2/2=120×√2/2=60√2

Площадь четырехугольника ADKE:
- Четырехугольник ADKE образован двумя из шести равновеликих треугольников.
- Следовательно, его площадь составляет 1/3 от общей площади треугольника:

Площадь ADKE=60√2/3=20√2

Ответ: Площадь четырехугольника ADKE равна 20√2 см².

Как найти длину медианы треугольника | Описание курса | Угол между высотой и медианой треугольника