|
|
Примечание. Это часть урока с задачами по геометрии (раздел стереометрия, задачи о пирамиде). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".
Задача.
Высота боковой грани правильной четырехугольной пирамиды равна 10 см.Определите полную поверхность пирамиды,если боковая грань наклонена к плоскости основания под углом 60.
Решение.
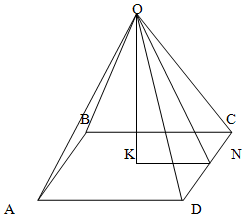
Поскольку угол ONK равен 60 градусам, то
KN = ON cos 60 = 10 * 1/2 = 5 см
Так как, по условию задачи, пирамида является правильной, то K - проецирется в центр основания, которое является квадратом. Значит сторона основания равна
AD = 2KN = 2 * 5 = 10 см
Таким образом, площадь основания
S1 = AD2 = 102 = 100 см2 .
Найдем площадь боковой грани
S2 = 1/2 CD * ON
S2 = 1/2 * 10 * 10 = 50 см2 .
Таким образом общая площадь
S = S1 + 4S2 = 100 + 4 * 50 = 300 см2 .
Ответ: 300 см2 .
Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании |
Описание курса
| Нахождение углов пирамиды
|

