|
|
Примечание. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак "√".
Задача.
Высота правильной треугольной пирамиды 4 см, а ее апофемы 8 см.
Вычислите площадь боковой поверхности пирамиды.
Решение.
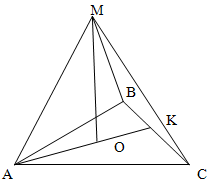
Исходя из того, что MK = 8, MO = 4, синус угла OKM равен
MO/MK = 1/2
откуда угол равен arcsin 1/2 = 30 градусов.
Откуда
KO / MK = cos 30
KO / 8 = cos 30
KO = 8 cos 30
По таблице тригонометрических функций найдем значение косинуса 30 градусов.
KO = 8√3/2 = 4√3
Учтем, что KO является радиусом вписанной окружности в основание правильной треугольной пирамиды (согласно свойствам правильной пирамиды). Тогда по свойству равностороннего треугольника (формула нахождения радиуса вписанной окружности, приведенная на рисунке)
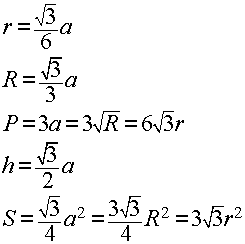
r = a√3/6
Подставим в формулу известное нам значение радиуса вписанной окружности, откуда найдем значение стороны равностороннего треугольника
4√3 = a√3/6
a = 24
Теперь, зная размер основания боковой грани и ее апофему, найдем площадь боковой грани как площадь равнобедренного треугольника:
Sт = 1/2 * 24 * 8 = 96 см2
Откуда площадь боковой поверхности пирамиды
S = 3 Sт = 3 * 96 = 288 см2 .
Ответ: 288 см2.
Площадь поверхности правильной треугольной пирамиды |
Описание курса
| Правильный тетраэдр (пирамида)
|

