|
Урок содержит описание свойств и формулы нахождения высоты треугольника, а также примеры решения задач. Если Вы не нашли решение подходящей задачи - пишите про это на форуме. Наверняка, курс будет дополнен.
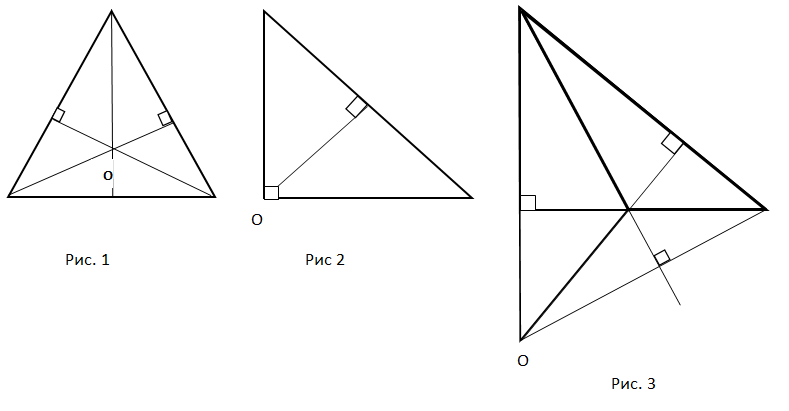
ВЫСОТА ТРЕУГОЛЬНИКА
Высота треугольника – опущенный из вершины треугольника перпендикуляр, проведенный на противолежащую вершине сторону или на ее продолжение.
Свойства высоты треугольника:
- Если в треугольнике две высоты равны, то такой треугольник - равнобедренный
- В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному
- В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащих на двух сторонах, непараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины этой стороны всегда можно провести окружность
- В остроугольном треугольнике две его высоты отсекают от него подобные треугольники
- Минимальная высота в треугольнике всегда проходит внутри этого треугольника
Ортоцентр треугольника
Все три высоты треугольника (проведенные из трех вершин) пересекаются в одной точке, которая называется ортоцентром. Для того, чтобы найти точку пересечения высот, достаточно провести две высоты (две прямые пересекаются только в одной точке).
Расположение ортоцентра (точка О) определяется видом треугольника.
У остроугольного треугольника точка пересечения высот находится в плоскости треугольника. (Рис.1).
У прямоугольного треугольника точка пересечения высот совпадает с вершиной прямого угла (Рис.2).
У тупоугольного треугольника точка пересечения высот находится за плоскостью треугольника (Рис.3).
У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают.
У равностороннего треугольника все три «замечательные» линии (высота, биссектриса и медиана) совпадают и три «замечательных» точки (точки ортоцентра, центра тяжести и центра вписанной и описанной окружностей) находятся в одной точке пересечения «замечательных» линий, т.е. тоже совпадают.
|
Формулы нахождения высоты треугольника
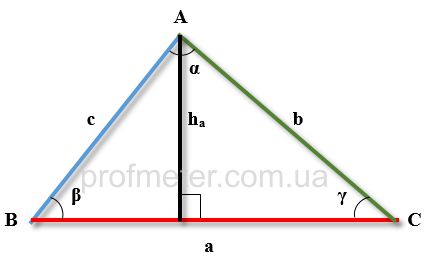
Рисунок приведен для облегчения восприятия формул нахождения высоты треугольника. Общее правило - длина стороны обозначена маленькой буквой, лежащей напротив соответствующего угла. То есть сторона a лежит напротив угла A.
Высота в формулах обозначается буквой h, нижний индекс которой соответствует стороне, на которую она опущена.
Другие обозначения:
a,b,c - длины сторон треугольника
ha - высота треугольника, проведенная к стороне a из противолежащего угла
hb - высота, проведенная к стороне b
hc - высота, проведенная к стороне c
R - радиус описанной окружности
r - радиус вписанной окружности
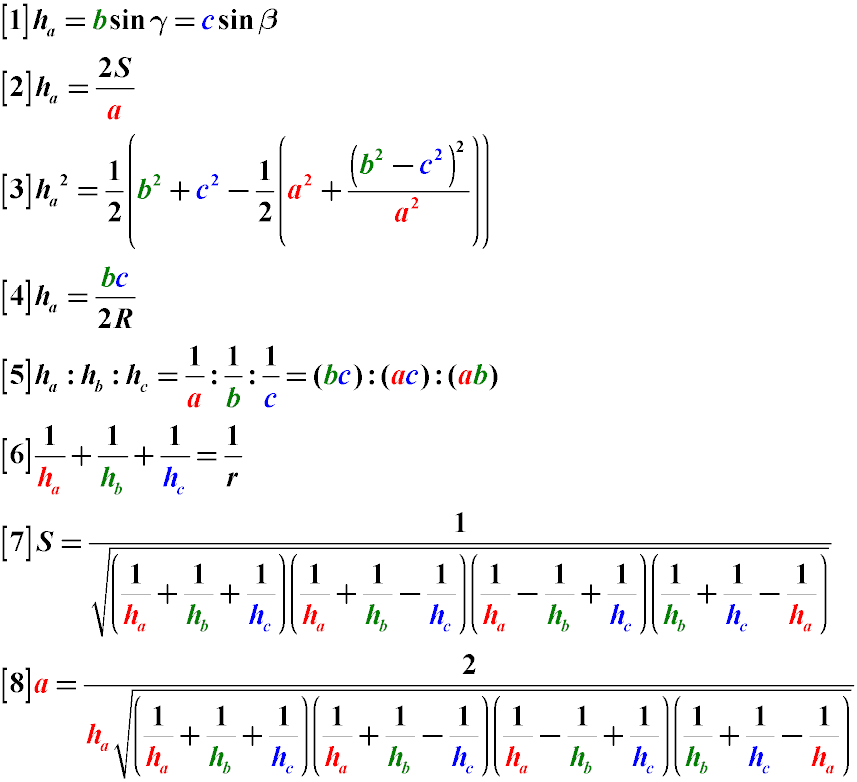
Пояснения к формулам.
Высота треугольника равна произведению длины стороны, прилежащей к углу, из которой опущена эта высота на синус угла между этой стороной и стороной, на которую такая высота опущена (Формула 1)
Высота треугольника равна частному от деления удвоенной величины площади треугольника на длину стороны, к которой опущена эта высота (Формула 2)
Высота треугольника равна частному от деления произведения сторон, прилежащих к углу, из которого опущена эта высота, на удвоенный радиус описанной вокруг него окружности (Формула 4).
Высоты сторон в треугольнике соотносятся между собой в той же самой пропорции, как соотносятся между собой обратные пропорции длин сторон этого же треугольника, а также в той же самой пропорции между собой относятся произведения пар сторон треугольника, которые имеют общий угол (Формула 5).
Сумма обратных значений высот треугольника равна обратному значению радиуса вписанной в такой треугольник окружности (Формула 6)
Площадь треугольника можно найти через длины высот этого треугольника (Формула 7)
Длину стороны треугольника, на которую опущена высота, можно найти через применение формул 7 и 2.
В прямоугольном треугольнике ABC (угол C = 900) проведена высота CD. Определите CD, если AD = 9 см, BD = 16 см
Решение.
Треугольники ABC, ACD и CBD подобны между собой . Это непосредственно следует из второго признака подобия (равенство углов в этих треугольниках очевидно).
Прямоугольные треугольники - единственный вид треугольников, которые можно разрезать на два треугольника, подобных между собой и исходному треугольнику.
Обозначения этих трех треугольников в таком порядке следования вершин: ABC, ACD, CBD. Тем самым мы одновременно показываем и соответствие вершин. (Вершине A треугольника ABC соответствует также вершина A треугольника ACD и вершина C треугольника CBD и т. д.)
Треугольники ABC и CBD подобны. Значит:
AD/DC = DC/BD, то есть
DC2=AD*BD
DC2=9*16
DC=12 см
Задача на применение теоремы Пифагора.
Треугольник ABC является прямоугольным. При этом C-прямой угол. Из него проведена высота CD=6см. Разность отрезков BD-AD=5 см.
Найти: Стороны треугольника ABC.
Решение.
1.Составим систему уравнений согласно теореме Пифагора
CD2+BD2=BC2
CD2+AD2=AC2
поскольку CD=6
36+BD2=BC2
36+AD2=AC2
Поскольку BD-AD=5, то
BD = AD+5, тогда система уравнений принимает вид
36+(AD+5)2=BC2
36+AD2=AC2
Сложим первое и второе уравнение. Поскольку левая часть прибавляется к левой, а правая часть к правой - равенство не будет нарушено. Получим:
36+36+(AD+5)2+AD2=AC2+BC2
72+(AD+5)2+AD2=AC2+BC2
2. Теперь, взглянув на первоначальный чертеж треугольника, по той же самой теореме Пифагора, должно выполняться равенство:
AC2+BC2=AB2
Поскольку AB=BD+AD, уравнение примет вид:
AC2+BC2=(AD+BD)2
Поскольку BD-AD=5, то BD = AD+5, тогда
AC2+BC2=(AD+AD+5)2
3. Теперь взглянем на результаты, полученные нами при решении в первой и второй части решения. А именно:
72+(AD+5)2+AD2=AC2+BC2
AC2+BC2=(AD+AD+5)2
Они имеют общую часть AC2+BC2 . Таким образом, приравняем их друг к другу.
72+(AD+5)2+AD2=(AD+AD+5)2
72+AD2+10AD+25+AD2=4AD2+20AD+25
-2AD2-10AD+72=0
В полученном квадратном уравнении дискриминант равен D=676, соответственно, корни уравнения равны:
х1=-3,5
x2=4
Поскольку длина отрезка не может быть отрицательной, отбрасываем первый корень.
AD=4
Соответственно
BD = AD + 5 = 9
AB = BD + AD = 4 + 9 = 13
По теореме Пифагора находим остальные стороны треугольника:
AC = корень из (52)
BC = корень из (117).
Треугольник |
Описание курса
| Сумма углов треугольника
|

