АКСИОМА 8

СУЩЕСТВОВАНИЕ ТРЕУГОЛЬНИКА, РАВНОГО ДАННОМУ

Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

Задав любое направление прямой, на ней можно всегда построить треугольник, равный данному.

Два треугольника могут отличаться друг от друга по длине сторон, по градусной мере углов, но их расположение на плоскости (ориентация)
не влияет на равенство или неравенство треугольников.

Треугольники называются равными, если у них соответствующие стороны и углы равны.

Дополнительные сведения

1. Копирование треугольника: Для построения треугольника, равного данному, можно использовать метод копирования. Это включает
   в себя измерение всех сторон и углов исходного треугольника и построение нового треугольника с такими же размерами.

2. Поворот и отражение: Равные треугольники могут быть получены путем поворота или отражения исходного треугольника. Эти
   операции не изменяют длины сторон и углы треугольника, поэтому полученные треугольники остаются равными исходному.

3. Практическое применение: В геометрии и инженерии часто требуется построение равных треугольников для различных задач, таких
   как создание симметричных конструкций или проверка правильности построений.

4. Теорема о равенстве треугольников: Существует несколько теорем, которые помогают определить равенство треугольников, такие
   как теорема о равенстве треугольников по трем сторонам (SSS), по двум сторонам и углу между ними (SAS), и по двум углам и стороне
   между ними (ASA).

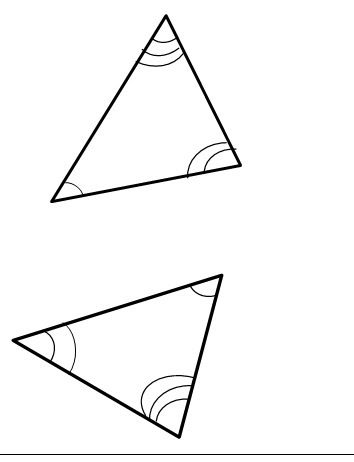
На рис. приведены равные треугольники, но по-разному ориентированные на плоскости.