|
См. также биссектриса угла.
БИССЕКТРИСА УГЛА ТРЕУГОЛЬНИКА
Биссектриса треугольника – отрезок биссектрисы угла, соединяющий вершину этого угла с точкой на противолежащей стороне.
У биссектрис угла треугольника есть масса свойств, которые описываются через свойства треугольника. Это поможет в решении задач.
Свойства биссектрис треугольника
-
Биссектриса треугольника, проведенная из данной вершины, тождественна биссектрисе соответствующего угла. Биссектриса угла треугольника, выходящая из его вершины, делит этот угол треугольника пополам
-
Все три биссектрисы треугольника пересекаются в одной точке, которая расположена всегда в плоскости треугольника и является центром вписанной окружности. Примечание. Имеются ввиду биссектрисы внутренних углов треугольника.

-
Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины

- Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные сторонам треугольника
- Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
-
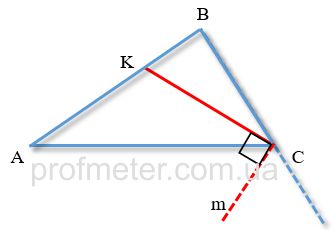
Угол между биссектрисами двух смежных углов (между внутренними и внешними биссектрисами углов треугольника при одной вершине) равен 90 градусам
Свойства биссектрис равнобедренного треугольника
-
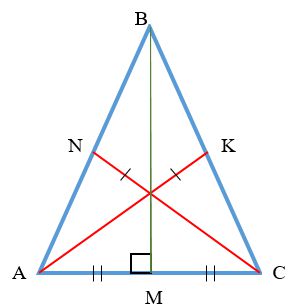
У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают
-
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит.
-
В равнобедренном треугольнике две биссектрисы равны, а третья биссектриса является его медианой и высотой
-
Одна и только одна биссектриса внешнего угла неравностороннего треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный
Свойства биссектрис равностороннего треугольника
Формулы нахождения биссектрисы угла
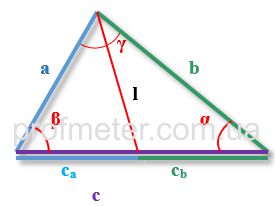
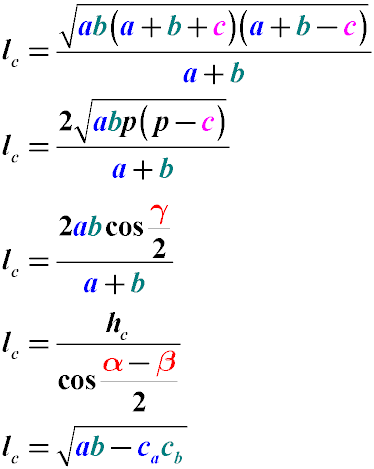
a, b, c - стороны треугольника, при этом биссектриса проведена из угла, находящегося между сторонами a, b
α,β,γ - углы треугольника, противолежащие сторонам a,b,c соответственно
p - полупериметр треугольника (половина суммы всех его сторон)
ca, cb - отрезки, на которые биссектрисой, проведенной из угла c разбита сторона c
lc - длина биссектрисы, проведенной к стороне c из угла γ.
Длина биссектрис треугольника может быть выражена через равенство с квадратом суммы всех его сторон.

Формулы нахождения расстояния от угла до точки пересечения биссектрис
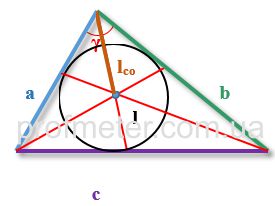
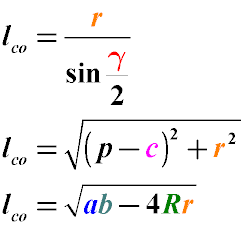
где
lco - длина отрезка, лежащего на биссектрисе от вершины угла до центра пересечения биссектрис
r - радиус окружности, вписанной в треугольник
R - радиус описанной окружности
a, b, c - стороны треугольника, при этом биссектриса проведена из угла, находящегося между сторонами a, b
γ - угол треугольника, противолежащий стороне c
p - полупериметр треугольника (половина суммы всех его сторон)
Примеры решения задач
Примечание. В данном уроке изложены задачи по геометрии о биссектрисе. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Почти наверняка курс будет дополнен.
Задача.
Луч AD является биссектрисой угла A. На сторонах угла A отмечены точки B,C так что угол ADC равен углу ADB. Доказать, что AB=AC.
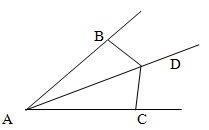
Решение.
Рассмотрим треугольники ADB и ADC. Сторона AD у них общая, углы DAC и DAB равны, так как биссектриса AD делит угол А пополам, а углы ADC и ADB равны по условию задачи. Таким образом, треугольники ADB и ADC равны по стороне и двум углам.
Следовательно AB = AC.
Биссектриса угла |
Описание курса
| Биссектриса внешнего угла
|

