Правильная пирамида - частный случай пирамиды.
Правильная пирамида. Определение
Определение 1. Пирамида называется правильной, если её основанием является правильный многоугольник, при этом вершина такой пирамиды проецируется в центр ее основания.
Определение 2. Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания.
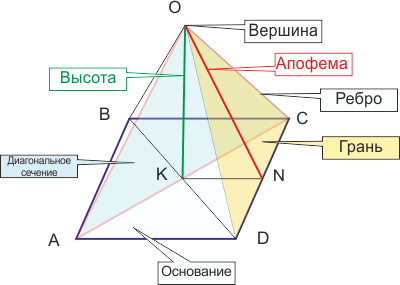
Элементы правильной пирамиды
- Высота боковой грани, проведенная из ее вершины называется апофема. На рисунке обозначена как отрезок ON
- Точка, соединяющая боковые рёбра и не лежащая в плоскости основания, называется вершиной пирамиды (О)
- Треугольники, имеющие общую сторону с основанием и одну из вершин, совпадающую с вершиной, называются боковыми гранями (AOD, DOC, COB, AOB)
- Отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания называется высотой пирамиды (ОК)
- Диагональное сечение пирамиды - это сечение, проходящее через вершину и диагональ основания (AOC, BOD)
- Многоугольник, которому не принадлежит вершина пирамиды, называется основанием пирамиды (ABCD)
Если в основании правильной пирамиды лежит треугольник, четырехугольник и т.д. то она называется правильной треугольной, четырехугольной и т.д.
Треугольная пирамида есть четырехгранник — тетраэдр.
Свойства правильной пирамиды
Для решения задач необходимо знать свойства отдельных элементов, которые в условии обычно опускаются, так как считается, что ученик должен это знать изначально.
- боковые ребра равны между собой
- апофемы равны
- боковые грани равны между собой (при этом, соответственно, равны их площади, боковые стороны и основания), то есть они являются равными треугольниками
- все боковые грани являются равными равнобедренными треугольниками
- в любую правильную пирамиду можно как вписать, так и описать около неё сферу
- если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна π, а каждый из них соответственно π/n, где n — количество сторон многоугольника основания
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
- около основания правильной пирамиды можно описать окружность (см. также радиус описанной окружности треугольника)
- все боковые грани образуют с плоскостью основания правильной пирамиды равные углы
- все высоты боковых граней равны между собой
Указания к решению задач. Свойства, перечисленные выше, должны помочь в практическом решении. Если требуется найти углы наклона граней, их поверхность и т. д., то общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для нахождения отдельных элементов пирамиды, поскольку многие элементы являются общими для нескольких фигур.
Необходимо разбить всю объемную фигуру на отдельные элементы - треугольники, квадраты, отрезки. Далее, к отдельным элементам применить знания из курса планиметрии, что существенно упрощает нахождение ответа.
Формулы для правильной пирамиды
Формулы для нахождения объема и площади боковой поверхности:
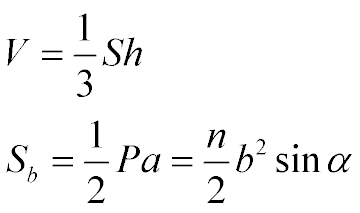
Обозначения:
V - объем пирамиды
S - площадь основания
h - высота пирамиды
Sb - площадь боковой поверхности
a - апофема (не путать с α)
P - периметр основания
n - число сторон основания
b - длина бокового ребра
α - плоский угол при вершине пирамиды
Данная формула нахождения объема может применяться только для правильной пирамиды:
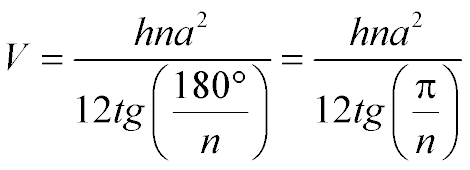 , где , где
V - объем правильной пирамиды
h - высота правильной пирамиды
n - число сторон правильного многоугольника, который является основанием для правильной пирамиды
a - длина стороны правильного многоугольника
Правильная усеченная пирамида
Если провести сечение, параллельное основанию пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Это сечение для усеченной пирамиды является одним из её оснований.
Высота боковой грани (которая является равнобокой трапецией), называется — апофема правильной усеченной пирамиды.
Усечённая пирамида называется правильной, если пирамида, из которой она была получена – правильная.
- Расстояние между основаниями усеченной пирамиды называется высотой усеченной пирамиды
- Все грани правильной усеченной пирамиды являются равнобокими (равнобедренными) трапециями
Примечания
См. также: частные случаи (формулы) для правильной пирамиды:
Как воспользоваться приведенными здесь теоретическими материалами для решения своей задачи:

- Ознакомьтесь со справочными материалами
- Выясните, по условию задачи, о какой именно правильной пирамиде идет речь
- После этого в дереве знаний справа, найдите подходящий урок с данной фигурой (см. решение задач про правильную пирамиду с треугольником в основании, с четырехугольником в основании). Если нужного решения не нашлось, попробуйте ознакомиться с содержанием соседних уроков, возможно, решение подобной задачи есть именно там
- Если Вы просмотрели весь раздел, но аналогичной задачи не нашлось, напишите о своей проблеме на форуме "раздел для школьников" в соответствующей теме. Обязательно ознакомьтесь предварительно с правилами форума.
Пирамида и вписанный конус |
Описание курса
| Апофема правильной пирамиды
|

