В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа - задайте вопрос на форуме.
Задача
Диагонали BD и AC трапеции ABCD пересекаются в точке O. Длина диагонали BD равна 40 см. Найдите величину отрезка ОD, если основания трапеции BC и ADотносятся как 3 к 7.
Решение.
Треугольники AOD и BOC являются подобными по трем углам - AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как 3 к 7. Таким образом:
BO / OD = 3 / 7
По условию задачи, BO + OD = 40, соответственно
OD = 40 - BO
Таким образом,
BO / ( 40 - BO ) = 3 / 7
7BO = 3 ( 40 - BO )
7BO = 120 - 3BO
10BO = 120
BO = 12
Соответственно, OD = 40 - 12 = 28
Ответ: 28 см
Задача
Разность оснований трапеции равна 4 см, а средняя линия 10 см. Найдите основания трапеции.
Решение.
Обозначим большее основание как а, а меньшее как b. Учтем при этом следующее:
Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме
Значит:
a - b = 4
(a + b) / 2 = 10
Откуда a = b + 4, тогда
(b + 4 + b) / 2 = 10
2b + 4 = 20
b = 8
Следовательно a = b + 4 = 12
Ответ: Основания трапеции равны 8 и 12 см
Задача
У трапеции ABCD угол ABC равен углу ACD. При этом величина основания AD равна 18 сантиметрам, а диагональ AC равна 12 см.
Найти величину основания BC.
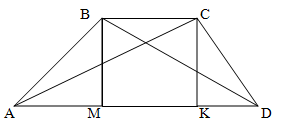
Решение.
Поскольку ABCD - трапеция, то углы CAD и BCA равны, исходя из свойств секущей для двух параллельных прямых.
Так как углы CAD и BCA равны, углы ABC и ACD равны по условию, то в треугольниках ABC и ACD, в которых два угла равны, третьи углы также равны - угол BAC равен CDA (сумма углов треугольника равна 180 градусам, а два из трех углов равны, поэтому и оставшиеся углы равны).
Так как все углы треугольников ABC и ACD попарно равны, то такие треугольники подобны.
Поскольку треугольники ABC и ACD подобны, то соотношения всех их сторон равны одному и тому же числу.
Откуда:
AC/AD = BC/AC
(AC - сторона, противолежащая углу B треугольника ABC, AD - сторона, противолежащая соответствующему углу треугольника ACD, аналогично и правой стороной равенства)
таким образом:
12/18 = BC/12
BC = 8
Ответ: BC = 8 см
Высота трапеции |
Описание курса
| Диагонали трапеции
|

