|
|
Пирамида
В данном разделе приведены формулы нахождения высоты, площади, объема пирамиды (в том числе усеченной). Описаны названия ее элементов (вершина, апофема, ребро, грань, высота, диагональное сечение).
В подразделах можно посмотреть примеры решения задач про пирамиды.
Объем пирамиды
Объем любой пирамиды (в т.ч. треугольной) равен одной трети произведения площади ее основания на высоту
Объем усеченной пирамиды
H – высота усеченной пирамиды; S1 – площадь нижнего основания; S2 – площадь верхнего основания.
Свойства правильной пирамиды
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Правильная пирамида имеет следующие свойства:
- боковые ребра правильной пирамиды равны;
- в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
- в любую правильную пирамиду можно как вписать сферу
- около любой правильной пирамиды можно описать сферу;
- если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна π, а каждый из них соответственно , где n — количество сторон многоугольника основания;
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Как найти площадь пирамиды
Площадь пирамиды (S) равна сумме площади ее основания (Sоснования) и боковой поверхности SБокПоверхности (Формула 1)
Соответственно, так как площадь боковой поверхности пирамиды равна сумме поверхностей всех ее граней (S1,S2...Sn), то получаем формулу 2.

Если пирамида правильная, то площади всех ее боковых граней равны между собой. Тогда достаточно найти площадь основания пирамиды и прибавить к нему площадь боковой грани (SГрани), умноженной на их количество (n) (см. Формулу 3).
Поскольку мы знаем, что в правильной пирамиде все грани представляют собой равнобедренный треугольник, то, использовав формулу площади равнобедренного треугольника, получим Формулу 4 - где площадь боковой поверхности пирамиды будет равна произведению половины периметра основания (P) на апофему (a).
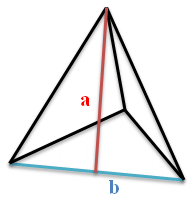
Для нахождения площади правильной треугольной пирамиды используем формулу площади равностороннего треугольника со стороной b, к которой прибавим площадь трех граней, представляющих собой равнобедренный треугольник с основанием b и высотой a (она же апофема правильной треугольной пирамиды). В итоге получаем Формулу 5.
Если же пирамида представляет собой тетраэдр, то все его грани равны между собой и площадь поверхности такой пирамиды равна квадрату стороны (b), умноженному на корень из трех (Формула 6).
Площадь поверхности правильной четырехугольной пирамиды находится по общему правилу - поскольку в основании лежит квадрат, то его площадь равна квадрату стороны основания (b), к которому прибавляется площадь четырех граней боковых сторон (Формула 7).
Ромб в основании призмы |
Описание курса
| С треугольником в основании
|

